题目内容
已知焦点F在x轴上的抛物线C经过定点P(3,2
),过F任意做C的弦AB,若弦AB的长不超8,且直线AB与椭圆3x2+2y2=2相交于不同的两点,求直线AB的倾斜角θ的取值范围.
| 3 |
考点:抛物线的简单性质
专题:圆锥曲线中的最值与范围问题
分析:由题意可设抛物线C的方程为y2=2px,(p>0),由抛物线C的标准方程y2=4x,可得焦点F(1,0).设直线l倾斜角为α,以下分类讨论:
(i)当直线l⊥x轴时,弦长|AB|=2p=4.满足题意:联立②联立
,无解,因此不满足条件直线l与椭圆3x2+2y2=2有公共点,故直线l倾斜角α≠
.
(ii)当直线l与x轴不垂直时,设直线l的方程为y=k(x-1).(k≠0).与抛物线的方程联立得到根与系数的关系,利用弦长公式|AB|=x1+x2+p≤8,得到k的一个范围;与椭圆的方程联立得到△>0,由得到k的一个范围,与上面的联立即可得出,进而得到α的取值范围.
(i)当直线l⊥x轴时,弦长|AB|=2p=4.满足题意:联立②联立
|
| π |
| 2 |
(ii)当直线l与x轴不垂直时,设直线l的方程为y=k(x-1).(k≠0).与抛物线的方程联立得到根与系数的关系,利用弦长公式|AB|=x1+x2+p≤8,得到k的一个范围;与椭圆的方程联立得到△>0,由得到k的一个范围,与上面的联立即可得出,进而得到α的取值范围.
解答:
解:设抛物线方程为y2=2px,代入P(3,2
),可得p=4,
∴抛物线方程为y2=4x;可得焦点F(1,0).
设直线l倾斜角为α,以下分类讨论:
(i)当直线l⊥x轴时,弦长|AB|=2p=4.满足:①|AB|≤8;
②联立
,无解,因此不满足条件直线l与椭圆3x2+2y2=2有不同的公共点,故直线l倾斜角α≠
.
(ii)当直线l与x轴不垂直时,设直线l的方程为y=k(x-1).(k≠0).
联立
,化为k2x2-(2k2+4)x+k2=0.
∴x1+x2=
,
∴|AB|=x1+x2+p=
+2≤8,化为k2≥1.①
联立
,化为(3+2k2)x2-4k2x+2k2-2=0,
若直线l与椭圆3x2+2y2=2有两个不同的交点,则△=16k4-4(3+2k2)(2k2-2)>0,化为k2<3,②.
联立①②可得:1≤k2<3,解得-
<k≤-1或1≤k<
.
∴
<α≤
或
≤α<
.
| 3 |
∴抛物线方程为y2=4x;可得焦点F(1,0).
设直线l倾斜角为α,以下分类讨论:
(i)当直线l⊥x轴时,弦长|AB|=2p=4.满足:①|AB|≤8;
②联立
|
| π |
| 2 |
(ii)当直线l与x轴不垂直时,设直线l的方程为y=k(x-1).(k≠0).
联立
|
∴x1+x2=
| 2k2+4 |
| k2 |
∴|AB|=x1+x2+p=
| 2k2+4 |
| k2 |
联立
|
若直线l与椭圆3x2+2y2=2有两个不同的交点,则△=16k4-4(3+2k2)(2k2-2)>0,化为k2<3,②.
联立①②可得:1≤k2<3,解得-
| 3 |
| 3 |
∴
| 2π |
| 3 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 3 |
点评:本题考查了抛物线的标准方程及其性质、直线与抛物线椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式、△>0、直线的斜率与倾斜角的关系等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
函数f(x)=ax-2+loga(x-1)(a>0且a≠1),在x∈[2,3]上的最大值与最小值之和为a,则a等于( )
| A、4 | ||
B、
| ||
| C、2 | ||
D、
|
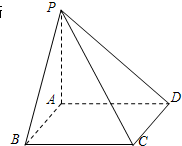 如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )
如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )| A、平面PAB⊥平面PAD |
| B、平面PAB⊥平面PBC |
| C、平面PBC⊥平面PCD |
| D、平面PCD⊥平面PAD |
已知函数f(x)=
,其中e是自然对数的底数,若直线y=2与函数y=f(x)的图象有三个交点,则常数a的取值范围是( )
|
| A、(-∞,2) |
| B、(-∞,2] |
| C、(2e-2,+∞) |
| D、[2e-2,+∞) |
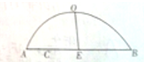 如图,A处为我军一炮兵阵地,距A处1000米的C处有一小山,山高为580米,在山的另一侧距C处3000米有敌武器库B,且A、B、C在同一水平直线删个,已知我炮兵轰击敌武器库是一段抛物线,这段抛物线的最大高度OE为800米.
如图,A处为我军一炮兵阵地,距A处1000米的C处有一小山,山高为580米,在山的另一侧距C处3000米有敌武器库B,且A、B、C在同一水平直线删个,已知我炮兵轰击敌武器库是一段抛物线,这段抛物线的最大高度OE为800米.