题目内容
已知在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,则直线AE与平面BDD1B1所成角的正切值是 .
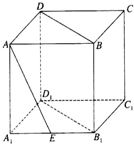

考点:直线与平面所成的角
专题:空间角
分析:首先利用转化法,求出线面所夹的角,进一步利用解三角形知识求出结果.
解答:
 解:已知在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,
解:已知在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,
连接AC交BD于O,做AB的中点F,连接B1F,取BO的中点G,连接FG,GB1
所以:B1F∥AE,FG⊥BD,
所以:AE与平面BDD1B1所成角为:∠FB1G
设正方体的棱长为1,
进一步求得:FG=
,B1G=
则:tan∠FB1G=
=
故答案为:
 解:已知在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,
解:已知在正方体ABCD-A1B1C1D1中,点E是棱A1B1的中点,连接AC交BD于O,做AB的中点F,连接B1F,取BO的中点G,连接FG,GB1
所以:B1F∥AE,FG⊥BD,
所以:AE与平面BDD1B1所成角为:∠FB1G
设正方体的棱长为1,
进一步求得:FG=
| ||
| 4 |
3
| ||
| 4 |
则:tan∠FB1G=
| FG |
| B1G |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查的知识要点:线面的夹角问题,解三角形知识的应用,属于基础题型.

练习册系列答案
相关题目
三个数a=0.22,b=log202,c=20.1之间的大小关系是( )
| A、a<c<b |
| B、a<b<c |
| C、b<a<c |
| D、b<c<a |
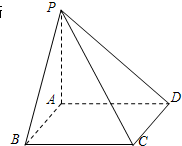 如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )
如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )| A、平面PAB⊥平面PAD |
| B、平面PAB⊥平面PBC |
| C、平面PBC⊥平面PCD |
| D、平面PCD⊥平面PAD |
已知函数f(x)=
,其中e是自然对数的底数,若直线y=2与函数y=f(x)的图象有三个交点,则常数a的取值范围是( )
|
| A、(-∞,2) |
| B、(-∞,2] |
| C、(2e-2,+∞) |
| D、[2e-2,+∞) |
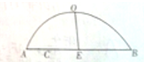 如图,A处为我军一炮兵阵地,距A处1000米的C处有一小山,山高为580米,在山的另一侧距C处3000米有敌武器库B,且A、B、C在同一水平直线删个,已知我炮兵轰击敌武器库是一段抛物线,这段抛物线的最大高度OE为800米.
如图,A处为我军一炮兵阵地,距A处1000米的C处有一小山,山高为580米,在山的另一侧距C处3000米有敌武器库B,且A、B、C在同一水平直线删个,已知我炮兵轰击敌武器库是一段抛物线,这段抛物线的最大高度OE为800米.