题目内容
若椭圆
+
=1的离心率为
，则双曲线
-
=1的离心率为 ．
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
考点：双曲线的简单性质,椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由已知中椭圆
+
=1的离心率为
，可得c2=
a2，进而b2=
a2，故在双曲线
-
=1中，c2=
a2，进而得到双曲线的离心率．
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| 4 |
| 9 |
| 5 |
| 9 |
| x2 |
| a2 |
| y2 |
| b2 |
| 14 |
| 9 |
解答：
解：∵椭圆
+
=1的离心率为
，
∴
=
，即c2=
a2，
∴b2=1-c2=
a2，
故在双曲线
-
=1中，
c2=a2+b2=a2+
a2=
a2，
∴
=
，
∴离心率e=
，
故答案为：
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
∴
| c2 |
| a2 |
| 4 |
| 9 |
| 4 |
| 9 |
∴b2=1-c2=
| 5 |
| 9 |
故在双曲线
| x2 |
| a2 |
| y2 |
| b2 |
c2=a2+b2=a2+
| 5 |
| 9 |
| 14 |
| 9 |
∴
| c2 |
| a2 |
| 14 |
| 9 |
∴离心率e=
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查的知识点是椭圆的简单性质，双曲线的简单性质，难度不大，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
等差数列{an}中，已知a1+a4+a7=39，则a4=（ ）
| A、13 | B、14 | C、15 | D、16 |
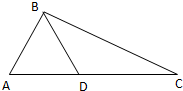
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=
BD，BC=2BD，则sinC的值为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图所示，正方体ABCD-A1B1C1D1的棱长为1，点M、N分别是面对角线A1B和B1D1的中点．在平行四边形ABCD中，
-
-
+
等于（ ）
| AB |
| AC |
| CA |
| CD |
A、2
| ||
B、
| ||
C、2
| ||
D、
|