题目内容
9．定义在（0，+∞）的函数f（x）满足2f（x）-（4-x）f′（x）＞0恒成立，则下列一定正确的是（ ）| A． | f（5）-f（3）＞0 | B． | f（6）-f（2）＜0 | C． | 4f（2）-f（3）＜0 | D． | 4f（6）-f（5）＞0 |
分析 由所给不等式2f（x）-（4-x）f′（x）＞0恒成立，构造辅助函数g（x）=（x-4）2f（x），由辅助函数求导，知g′（x）=（x-4）[2f（x）-（4-x）f′（x）]，与所给不等式有关，所以由辅助函数的单调性可知对应的f（x）的值的大小．
解答 解：∵2f（x）-（4-x）f′（x）＞0，
∴作辅助函数g（x）=（x-4）2f（x），
则g′（x）=（x-4）[2f（x）-（4-x）f′（x）]，
当x＞4时，有x-4＞0，2f（x）-（4-x）f′（x）＞0，
∴g（x）在[4，+∞）上是增函数．
∴当5＜6时，有g（5）＜g（6），即f（5）＜4f（6），
∴4f（6）-f（5）＞0．
故选：D．
点评 本题考查由所给不等式，构造辅助函数，对辅助函数求导，知与所给不等式有关，所以由辅助函数的单调性可知对应的f（x）的值的大小．属于好题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
17．给定集合An={1，2，3，…，n}，n∈N*．若f是An→An的映射且满足：
①任取i，j∈An，若i≠j，则f（i）≠f（j）；
②任取m∈An，若m≥2，则有m∈{f（1），f（2），…，f（m）}．
则称映射f为An→An的一个“优映射”．
例如：用表1表示的映射f：A3→A3是一个“优映射”．
表一
表2
（1）若f：A4→A4是一个“优映射”，请把表2补充完整（只需填出一个满足条件的映射）；
（2）若f：A2015→A2015是“优映射”，且f（1004）=1，则f（1000）+f（1017）的最大值为2021．
①任取i，j∈An，若i≠j，则f（i）≠f（j）；
②任取m∈An，若m≥2，则有m∈{f（1），f（2），…，f（m）}．
则称映射f为An→An的一个“优映射”．
例如：用表1表示的映射f：A3→A3是一个“优映射”．
表一
| i | 1 | 2 | 3 |
| F（i） | 2 | 3 | 1 |
| i | 1 | 2 | 3 | 4 |
| F（i） | 3 |
（2）若f：A2015→A2015是“优映射”，且f（1004）=1，则f（1000）+f（1017）的最大值为2021．
4．
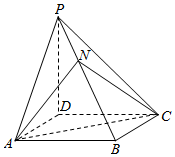如图，四棱锥P-ABCD的底面ABCD为平行四边形，NB=2PN，则三棱锥N-PAC与三棱锥D-PAC的体积比为（ ）
如图，四棱锥P-ABCD的底面ABCD为平行四边形，NB=2PN，则三棱锥N-PAC与三棱锥D-PAC的体积比为（ ）| A． | 1：2 | B． | 1：8 | C． | 1：6 | D． | 1：3 |
14．已知数列{an}是首项和公差相等的等差数列，其前n项和为Sn，且S10=55．
（Ⅰ）求an和Sn；
（Ⅱ）设${b_n}=\frac{1}{S_n}$，数列{bn}的前项和Tn，求Tn的取值范围．
（Ⅰ）求an和Sn；
（Ⅱ）设${b_n}=\frac{1}{S_n}$，数列{bn}的前项和Tn，求Tn的取值范围．
1．已知函数f（x）=2016x+log2016（$\sqrt{{x^2}+1$+x）-2016-x+2，则关于x的不等式f（3x+1）+f（x）＞4的解集为（ ）
| A． | （-$\frac{1}{4}$，+∞） | B． | （-∞，-$\frac{1}{4}$） | C． | （0，+∞） | D． | （-∞，0） |
如图，是某铁路客运部门设计的甲、乙两地之间旅客托运行李的费用c（单位：元）与行李重量w（单位：千克）之间的流程图．假定某旅客的托运费为10元，则该旅客托运的行李重量为20千克．