题目内容
17.给定集合An={1,2,3,…,n},n∈N*.若f是An→An的映射且满足:①任取i,j∈An,若i≠j,则f(i)≠f(j);
②任取m∈An,若m≥2,则有m∈{f(1),f(2),…,f(m)}.
则称映射f为An→An的一个“优映射”.
例如:用表1表示的映射f:A3→A3是一个“优映射”.
表一
| i | 1 | 2 | 3 |
| F(i) | 2 | 3 | 1 |
| i | 1 | 2 | 3 | 4 |
| F(i) | 3 |
(2)若f:A2015→A2015是“优映射”,且f(1004)=1,则f(1000)+f(1017)的最大值为2021.
分析 (1)根据“优映射”的定义可得,
| i | 1 | 2 | 3 | 4 |
| f(i) | 2 | 3 | 1 | 4 |
| i | 1 | 2 | 3 | 4 |
| f(i) | 2 | 3 | 4 | 1 |
(2)根据题意可得 只有当f(1000)=1004,f(101)=101时,f(1000)+f(1007)取得最大值.
解答 解:(1)
| i | 1 | 2 | 3 | 4 |
| f(i) | 2 | 3 | 1 | 4 |
| i | 1 | 2 | 3 | 4 |
| f(i) | 2 | 3 | 4 | 1 |
(2)根据优影射的定义,f:A2010→A2010是“优映射”,且f(1004)=1,则 对f(1000)+f(1007),
只有当f(1000)=1004,f(1017)=1017,f(1000)+f(1017)取得最大值为 1004+1017=2021,
故答案为:2021.
点评 本题考查映射的定义,“优映射”的定义,判断f(1)≠1,是解题的关键,是一道不错的创新题,属中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
9.定义在(0,+∞)的函数f(x)满足2f(x)-(4-x)f′(x)>0恒成立,则下列一定正确的是( )
| A. | f(5)-f(3)>0 | B. | f(6)-f(2)<0 | C. | 4f(2)-f(3)<0 | D. | 4f(6)-f(5)>0 |
6.设复数z=$\frac{2-i}{1+i}$(i为虚数单位),则|z|=( )
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
7.已知复数z=$\frac{3-i}{1+ai}$是纯虚数,则实数a=( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
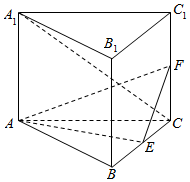 如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.
如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.