题目内容
14.已知数列{an}是首项和公差相等的等差数列,其前n项和为Sn,且S10=55.(Ⅰ)求an和Sn;
(Ⅱ)设${b_n}=\frac{1}{S_n}$,数列{bn}的前项和Tn,求Tn的取值范围.
分析 (1)S10=a1+a2+…+a10=55,求得55d=55,可解得a1=d=1,写出通项公式和前n项和公式;
(2)由(1)写出数列{bn}的通项公式,采用裂项法求出Tn的值,可判断Tn的取值范围.
解答 解:(Ⅰ)设数列{an}的公差为d,则a1=d,an=a1+(n-1)d=nd,
由S10=a1+a2+…+a10=55d=55,解得d=1,
所以an=n,则${S_n}=\frac{1+n}{2}×n=\frac{1}{2}n(n+1)$.(4分)
(Ⅱ)可得${b_n}=\frac{2}{n(n+1)}=2(\frac{1}{n}-\frac{1}{n+1})$,(6分)
所以${T_n}=2(\frac{1}{1}-\frac{1}{2})+2(\frac{1}{2}-\frac{1}{3})+2(\frac{1}{3}-\frac{1}{4})+…+2({\frac{1}{n}-\frac{1}{n+1}})=2(1-\frac{1}{n+1})=\frac{2n}{n+1}$,(8分)
由于$2(1-\frac{1}{n+1})$为随n的增大而增大,可得1≤Tn<2.
即Tn的取值范围是[1,2).(12分)
点评 本题考查等差数列的通项公式和前n项和公式及采用裂项法求数列的前n项和,过程简单,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
17.已知A={y|y=$\sqrt{l{n}^{2}x-2lnx+3}$,x≥1},B={x||lnx|≥1},则A∩B=( )
| A. | ($\sqrt{2}$,+∞) | B. | (1,$\frac{1}{e}$) | C. | [e,+∞) | D. | (e,+∞) |
9.定义在(0,+∞)的函数f(x)满足2f(x)-(4-x)f′(x)>0恒成立,则下列一定正确的是( )
| A. | f(5)-f(3)>0 | B. | f(6)-f(2)<0 | C. | 4f(2)-f(3)<0 | D. | 4f(6)-f(5)>0 |
6.设复数z=$\frac{2-i}{1+i}$(i为虚数单位),则|z|=( )
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
4.已知函数f(x)=2x-2,g(x)=ax(x-2a)同时满足条件:①?x∈R,f(x)<0或g(x)<0;②?x∈(-∞,-4),使得f(x)g(x)<0,则实数a的取值范围是( )
| A. | (-2,0) | B. | (-∞,-2) | C. | (-8,0) | D. | (0,2) |
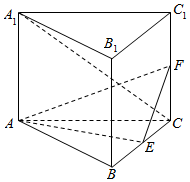 如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.
如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.