题目内容
4．
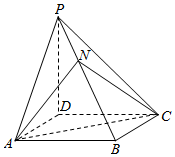如图，四棱锥P-ABCD的底面ABCD为平行四边形，NB=2PN，则三棱锥N-PAC与三棱锥D-PAC的体积比为（ ）| A． | 1：2 | B． | 1：8 | C． | 1：6 | D． | 1：3 |
分析 根据两个棱锥的底面和高与棱锥P-ABC的底面与高的关系得出两棱锥的体积与棱锥P-ABC的关系，得出答案．
解答 解：∵四边形ABCD是平行四边形，∴S△ABC=S△ACD．
∴VD-PAC=VP-ACD=VP-ABC．
∵NB=2PN，∴NB=$\frac{2}{3}$PB，
∴VN-ABC=$\frac{2}{3}$VP-ABC，
∴VN-PAC=VP-ABC-VN-ABC=$\frac{1}{3}$VP-ABC．
∴$\frac{{V}_{N-ABC}}{{V}_{D-PAC}}=\frac{1}{3}$．
故选：D．
点评 本题考查了棱锥的体积计算，寻找各棱锥的底面与高的关系是解题关键，属于基础题．
练习册系列答案
相关题目
7．C331+C332+C333+…+C3333除以9的余数是（ ）
| A． | 7 | B． | 0 | C． | -1 | D． | -2 |
9．定义在（0，+∞）的函数f（x）满足2f（x）-（4-x）f′（x）＞0恒成立，则下列一定正确的是（ ）
| A． | f（5）-f（3）＞0 | B． | f（6）-f（2）＜0 | C． | 4f（2）-f（3）＜0 | D． | 4f（6）-f（5）＞0 |
14．设F1，F2为双曲线$\frac{{x}^{2}}{4}-{y}^{2}$=1的两个焦点，P是双曲线上任意一点，且∠F1PF2=60°，则△PF1F2的面积是（ ）
| A． | 2$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | 3$\sqrt{3}$ |