题目内容
1.下列函数中,既不是奇函数也不是偶函数的是( )| A. | y=lnx | B. | y=|x| | C. | y=-x3 | D. | y=ex+e-x |
分析 根据奇偶函数的定义,可得结论.
解答 解:根据奇偶函数的定义,可得B,D为偶函数,C为奇函数,A既不是奇函数也不是偶函数.
故选:A.
点评 本题考查奇偶函数的定义,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
14.设函数f(x)=sin(2x+$\frac{π}{6}$)(x∈[0,$\frac{7π}{6}$]),若方程f(x)=m恰好有三个根,分别为x1,x2,x3(x1<x2<x3),则x1+2x2+x3的值是( )
| A. | $\frac{3π}{4}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{3π}{2}$ |
9.已知命题p:若a>1,则ax>logax恒成立;命题q:$f(x)=\left\{\begin{array}{l}\frac{1}{x}({x>0})\\{e^x}({x≤0})\end{array}\right.$,若F(x)=f(x)+x,x∈R,则F(x)的值域是(-∞,1]∪[2,+∞).下列选项为真命题的是( )
| A. | (¬p)∧(¬q) | B. | p∨(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
11.记方程①x2+a1x+1=0,②x2+a2x+1=0,③x2+a3x+1=0,其中a1,a2,a3是正实数,当a1,a2,a3成等比数列,下列选项中,当方程③有实根时,能推出的是( )
| A. | 方程①有实根或方程②无实根 | B. | 方程①有实根或方程②有实根 | ||
| C. | 方程①无实根或方程②无实根 | D. | 方程①无实根或方程②有实根 |
 已知函数g(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$,ω>0)的图象如图所示,函数f(x)=g(x)+$\frac{\sqrt{3}}{2}$cos2x-$\frac{3}{2}$sin2x
已知函数g(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$,ω>0)的图象如图所示,函数f(x)=g(x)+$\frac{\sqrt{3}}{2}$cos2x-$\frac{3}{2}$sin2x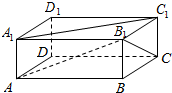 如图所示,ABCD-A1B1C1D1是长方体,AA1=a,∠BAB1=∠B1A1C1=30°,则AB与A1C1所成的角为30°,AA1与B1C所成的角为45°.
如图所示,ABCD-A1B1C1D1是长方体,AA1=a,∠BAB1=∠B1A1C1=30°,则AB与A1C1所成的角为30°,AA1与B1C所成的角为45°.