题目内容
在△ABC中，cosA=
，AC=3AB，则cosB= ．
| 1 |
| 3 |
考点：余弦定理,正弦定理
专题：三角函数的求值
分析：利用余弦定理表示出cosA，将b=3c代入用c表示出a，再利用余弦定理表示出cosB，将各自的值代入计算即可求出值．
解答：
解：∴cosA=
=
，
∴将b=3c代入得：
=
，
整理得：a=2
c，
∴cosB=
=
=0．
故答案为：0
| b2+c2-a2 |
| 2bc |
| 1 |
| 3 |
∴将b=3c代入得：
| 9c2+c2-a2 |
| 6c2 |
| 1 |
| 3 |
整理得：a=2
| 2 |
∴cosB=
| a2+c2-b2 |
| 2ac |
| 8c2+c2-9c2 | ||
4
|
故答案为：0
点评：此题考查了余弦定理，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
若U={1，2，3，4，5，6，7，8}，A={1，2，3}，B={5，6，7}，则（∁UA）∩（∁UB）=（ ）
| A、{4，8} |
| B、{2，4，6，8} |
| C、{1，3，5，7} |
| D、{1，2，3，5，6，7} |
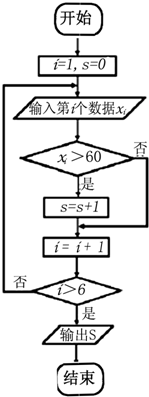某学生一个学期的数学测试成绩一共记录了6个数据：x1=52，x2=70，x3=68，x4=55，x5=85，x6=90，执行如图所示的程序框图，那么输出的S是（ ）