题目内容
在空间直角坐标系中有单位正方体ABCD-A1B1C1D1,则点C1到平面A1BD的距离为 .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:以D为原点,以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,利用向量法能求出点C1到平面A1BD的距离.
解答:
 解:以D为原点,以DA为x轴,以DC为y轴,以DD1为z轴,
解:以D为原点,以DA为x轴,以DC为y轴,以DD1为z轴,
建立空间直角坐标系,
则D(0,0,0),A1(1,0,1),B(1,1,0),C1(0,1,1),
∴
=(1,0,1),
=(1,1,0),
设平面A1BD的法向量
=(x,y,z),
则
,取x=1,得
=(1,-1,-1),
∵
=(0,1,1),
∴点C1到平面A1BD的距离d=
=
=
.
故答案为:
.
 解:以D为原点,以DA为x轴,以DC为y轴,以DD1为z轴,
解:以D为原点,以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,
则D(0,0,0),A1(1,0,1),B(1,1,0),C1(0,1,1),
∴
| DA1 |
| DB |
设平面A1BD的法向量
| n |
则
|
| n |
∵
| DC1 |
∴点C1到平面A1BD的距离d=
|
| ||||
|
|
| |0-1-1| | ||
|
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知F1,F2是椭圆C的两个焦点,焦距为4.若P为椭圆C上一点,且△PF1F2的周长为14,则椭圆C的离心率e为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
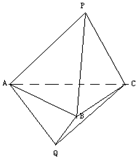 如图,在六面体PABCQ中,QA=QB=QC=AB=CB=CA=
如图,在六面体PABCQ中,QA=QB=QC=AB=CB=CA=