题目内容
13.已知cos2α=-$\frac{9}{41}$,cos2β=-$\frac{12}{13}$,$\frac{π}{2}$<α<π,$\frac{π}{2}$<β<π,求:sin2(α+β)-sin2(α-β)的值.分析 由条件利用同角三角函数的基本关系求得sin2α、cos2β的值,再利用两角和差的正弦公式、平方差公式以及二倍角公式,求得要求式子的值.
解答 解:∵cos2α=-$\frac{9}{41}$,cos2β=-$\frac{12}{13}$,$\frac{π}{2}$<α<π,$\frac{π}{2}$<β<π,
∴π<2α<2π,π<2β<2π,∴sin2α=-$\sqrt{{1-cos}^{2}2α}$=-$\frac{40}{41}$,sin2β=-$\sqrt{{1-cos}^{2}2β}$=-$\frac{5}{13}$,
∴sin2(α+β)-sin2(α-β)=[sin(α+β)+sin(α-β)]•[sin(α+β)-sin(α-β)]
[(sinαcosβ+cosαsinβ)+(sinαcosβ-cosαsinβ)]
•[(sinαcosβ+cosαsinβ)-(sinαcosβ-cosαsinβ]
=2sinαcosβ•2cosαsinβ=sin2α•sin2β=-$\frac{40}{41}$•(-$\frac{5}{13}$)=$\frac{200}{533}$.
点评 本题主要考查同角三角函数的基本关系,两角和差的正弦公式、平方差公式以及二倍角公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.过y2=2px焦点F的直线交抛物线于A,B,若|BF|=$\frac{6}{5}$,|AF|=$\frac{6}{7}$,则抛物线方程( )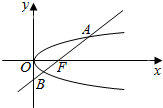

| A. | y2=x | B. | y2=2x | C. | y2=3x | D. | y2=4x |
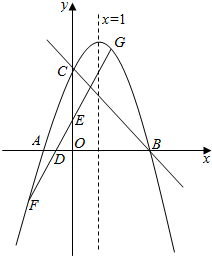 如图,对称轴为直线x=1的抛物线交x轴于点A、B,交y轴于点C(0,3),且S△ABC=6.
如图,对称轴为直线x=1的抛物线交x轴于点A、B,交y轴于点C(0,3),且S△ABC=6. 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,AB⊥BC,PA=6,AB=BC=8,DF=5.
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,AB⊥BC,PA=6,AB=BC=8,DF=5.