题目内容
5.已知复数A=z1$\overline{{z}_{2}}$+z2$\overline{{z}_{1}}$,B=z1$\overline{{z}_{1}}$+z2$\overline{{z}_{2}}$,其中z1,z2是非零复数,问:A,B可以比较大小?并证明之.分析 设z1=a+bi,z2=c+di(a,b,c,d∈R),根据共轭复数和复数的混合运算求出A,B,由于A、B都是实数,所以A、B可以比较大小,利用作差法即可比较大小.
解答 解:设z1=a+bi,z2=c+di(a,b,c,d∈R),
则A=z1$\overline{{z}_{2}}$+z2$\overline{{z}_{1}}$=(a+bi)(c-di)+(c+di)(a-bi)=2(acac+bd)∈R,
B=z1$\overline{{z}_{1}}$+z2$\overline{{z}_{2}}$=a2+b2+c2+d2∈R,
由于A、B都是实数,所以A、B可以比较大小.
又B-A=a2+b2+c2+d2-2(acac+bd)=(a-c)2+(b-d)2≥0,
于是得到A≤B,当且仅当a=c且b=d,即z1=z2时,取等号.
点评 本题考查了复数的混合运算和共轭复数的问题,以及比较大小,属于基础题.

练习册系列答案
相关题目
16.若向量$\overrightarrow{a}$=(2,3,λ),$\overrightarrow{b}$=(-1,1,$\frac{\sqrt{6}}{3}$)的夹角为60°,则λ等于( )
| A. | $\frac{23}{12}$ | B. | $\frac{\sqrt{6}}{12}$ | C. | $\frac{23\sqrt{6}}{12}$ | D. | -$\frac{23\sqrt{6}}{12}$ |
4.设集合A={0,1},集合B={x|x>a},若A∩B只有一个元素,则实数a的取值范围是( )
| A. | {a|a<1} | B. | {a|a≥1} | C. | {a|0≤a<1} | D. | {a|a≤1} |
8.已知全集A={x∈N|x<2},B={0,1,2},则A∩B=( )
| A. | {1,2} | B. | {0,1,2} | C. | {1} | D. | {0,1} |
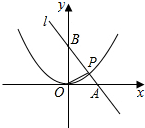 如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=ax2在第一象限内交于P点,如果△AOP的面积为2,求此抛物线的解析式.
如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=ax2在第一象限内交于P点,如果△AOP的面积为2,求此抛物线的解析式.