题目内容
18.已知函数f(x)=3sin($\frac{k}{5}x$+$\frac{π}{3}$)(k>0,k∈Z)有一条对称轴x=$\frac{π}{6}$,且在任意两整数间至少出现一次最大值和最小值,求k的最小取值.分析 先由对称轴x=$\frac{π}{6}$,可得$\frac{k}{5}×\frac{π}{6}+\frac{π}{3}$=mπ+$\frac{π}{2}$,解得:k=30m+5,m∈Z,根据在任意两个整数之间(包括正整数本身)变化时,函数f(x)至少有一个最大值和最小值,可确定函数f(x)的最小正周期的范围,再由正弦函数的最小正周期的求法可得到k的取值范围,进而可得到答案.
解答 解:∵函数f(x)=3sin($\frac{k}{5}x$+$\frac{π}{3}$)(k>0,k∈Z)有一条对称轴x=$\frac{π}{6}$,
∴$\frac{k}{5}×\frac{π}{6}+\frac{π}{3}$=mπ+$\frac{π}{2}$,m∈Z,
∴解得:k=30m+5,m∈Z①,
为使得函数f(x)=3sin($\frac{k}{5}x$+$\frac{π}{3}$),其中k>0,k∈Z在任意两个整数之间变化时,函数f(x)至少有一个最大值和最小值.
则函数f(x)的最小正周期一定不大于2,
∴T=$\frac{2π}{\frac{k}{5}}$=$\frac{10π}{k}$≤2,
∴k≥5π≈5×3.14=15.7②,
∴由①②即可解得k的最小自然数为35.
点评 本题主要考查正弦函数的基本性质--周期性.三角函数是高考的一个重要考点,并且对三角函数的考查一般以基础题为主,一定要强化基础知识的夯实,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
9.已知函数f(x)=asinx-$\sqrt{3}$cosx的一条对称轴为x=-$\frac{π}{6}$,且f(x1)•f(x2)=-4,则下列结论正确的是( )
| A. | a=±1 | B. | f(x1+x2)=0 | ||
| C. | |x1+x2|的最小值为$\frac{2π}{3}$ | D. | f(x)的最小正周期为2|x1-x2| |
4.设集合A={0,1},集合B={x|x>a},若A∩B只有一个元素,则实数a的取值范围是( )
| A. | {a|a<1} | B. | {a|a≥1} | C. | {a|0≤a<1} | D. | {a|a≤1} |
1.集合A={x|y=lg(-x2+2x)},B={x||x|≤1},则A∩B=( )
| A. | {x|1≤x≤2} | B. | {x|0<x≤1} | C. | {x|-1≤x≤0} | D. | {x|x≤2} |
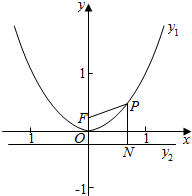 如图所示,在平面直角坐际系中有一抛物线y1=ax2,且抛物线经过点(2a-1,1),y轴上有一定点F,其坐标为(0,$\frac{1}{4}$),直线1的解析式为y2=-$\frac{1}{4}$,在抛物线上有一动点P,连接PF,并过点P作PN⊥直线1.
如图所示,在平面直角坐际系中有一抛物线y1=ax2,且抛物线经过点(2a-1,1),y轴上有一定点F,其坐标为(0,$\frac{1}{4}$),直线1的解析式为y2=-$\frac{1}{4}$,在抛物线上有一动点P,连接PF,并过点P作PN⊥直线1.