题目内容
3.有下列四个命题:①若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则$\overrightarrow{a}$=0或$\overrightarrow{b}$=0;
②对任意两个单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,都有$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$≤1;
③$\overrightarrow{a}•\overrightarrow{b}$>0?$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角;
④|$\overrightarrow{a}$|=|$\overrightarrow{b}$?|$\overrightarrow{a}•\overrightarrow{c}$|=|$\overrightarrow{b}•\overrightarrow{c}$|.
其中正确的命题是( )
| A. | ①③④ | B. | ①③ | C. | ② | D. | ①②④ |
分析 举例说明①③④错误;由向量的数量积运算说明②正确.
解答 解:①若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则$\overrightarrow{a}$=$\overrightarrow{0}$或$\overrightarrow{b}$=$\overrightarrow{0}$,错误,当$\overrightarrow{a},\overrightarrow{b}$均不为$\overrightarrow{0}$但$\overrightarrow{a}⊥\overrightarrow{b}$时仍有$\overrightarrow{a}$•$\overrightarrow{b}$=0;
②对任意两个单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,设其夹角为θ,有$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$=$|\overrightarrow{{e}_{1}}|•|\overrightarrow{{e}_{2}}|cosθ=cosθ$≤1,故②正确;
③若$\overrightarrow{a},\overrightarrow{b}$均为非零向量且同向,则$\overrightarrow{a}•\overrightarrow{b}>0$,故$\overrightarrow{a}•\overrightarrow{b}$>0?$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角错误;
④若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,但$\overrightarrow{a}$,$\overrightarrow{b}$与$\overrightarrow{c}$的夹角的余弦值的绝对值不等,则|$\overrightarrow{a}•\overrightarrow{c}$|≠|$\overrightarrow{b}•\overrightarrow{c}$|,故④错误.
∴其中正确的命题是②.
故选:C.
点评 本题考查命题的真假判断与应用,考查了平面向量的基本概念及数量积运算,是中档题.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案| A. | $\frac{4\sqrt{3}}{3}$ | B. | $-\frac{4\sqrt{3}}{3}$ | C. | 4$\sqrt{3}$ | D. | $-4\sqrt{3}$ |
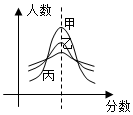 某市期末教学质量检测,甲、乙、丙三科考试成绩近似服从正态分布,则由如图曲线可得下列说法中错误的是( )
某市期末教学质量检测,甲、乙、丙三科考试成绩近似服从正态分布,则由如图曲线可得下列说法中错误的是( )| A. | 甲、乙、丙的总体的均值都相同 | B. | 甲学科总体的方差最小 | ||
| C. | 乙学科总体的方差及均值都居中 | D. | 丙学科总体的方差最大 |