题目内容
17.已知△ABC中,a=3,b=3$\sqrt{3}$,A=30°,则B等于( )| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
分析 利用正弦定理求出sinB,得出B,利用内角和定理进行检验.
解答 解:由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,即$\frac{3}{\frac{1}{2}}=\frac{3\sqrt{3}}{sinB}$,
∴sinB=$\frac{\sqrt{3}}{2}$.
∴B=60°或B=120°.
故选:D.
点评 本题考查了正弦定理,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.在△ABC中,M1,M2分别是边BC,AC的中点,AM1与BM2相交于点G,BC的垂直平分线与AB交于点N,且$\overrightarrow{NG}$•$\overrightarrow{NC}$-$\overrightarrow{NG}$•$\overrightarrow{NB}$=$\frac{1}{6}$$\overrightarrow{BC}$2,则△ABC是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 任意三角形 |
8.执行如图所示的程序框图,输出S的值是( )


| A. | 0 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
12.执行如图的程序框图,如果输入的t∈[-1,π],则输出的S属于( )
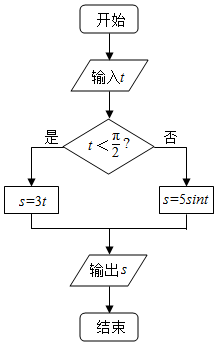

| A. | $[-3,\frac{3π}{2}]$ | B. | $[-5,\frac{3π}{2}]$ | C. | [-5,5] | D. | [-3,5] |
9.双曲线15y2-x2=15与椭圆$\frac{x^2}{25}+\frac{y^2}{9}$=1的( )
| A. | 焦点相同 | B. | 焦距相同 | C. | 离心率相等 | D. | 形状相同 |