题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为e=
,过右焦点作垂直于x轴的直线与椭圆相交于两点,且两交点与椭圆的左焦点及右顶点构成的四边形面积为
+4.
(1)求椭圆的方程;
(2)过点B(-2,0)的直线l与椭圆C交于P,Q两点,交圆O:x2+y2=8于M,N两点,若|MN|∈[4,2
],求△OPQ面积的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 5 |
8
| ||
| 5 |
(1)求椭圆的方程;
(2)过点B(-2,0)的直线l与椭圆C交于P,Q两点,交圆O:x2+y2=8于M,N两点,若|MN|∈[4,2
| 7 |
考点:直线与圆锥曲线的综合问题,椭圆的简单性质,圆与圆锥曲线的综合
专题:圆锥曲线中的最值与范围问题
分析:对第(1)问,由离心率e的值,得a,c的关系式,由面积易得a,b,c的关系式,联立c2=a2-b2,即可得a,b的值.
对第(2)问,先设出直线l的方程,与圆的方程联立,消去x,得到一个关于y的一元二次方程,由韦达定理及弦长公式,得弦长|MN|的表达式,由|MN|∈[4,2
],得m的取值范围;联立直线l与抛物线C的方程,消去x,同样得到一个关于y的另一个一元二次方程,由韦达定理及弦长公式,得弦长|PQ|的表达式,再用m表示原点O到直线l的距离d,即得△POQ面积的表达式,通过m的范围可探究△POQ面积的取值范围.
对第(2)问,先设出直线l的方程,与圆的方程联立,消去x,得到一个关于y的一元二次方程,由韦达定理及弦长公式,得弦长|MN|的表达式,由|MN|∈[4,2
| 7 |
解答:
解:(1)设椭圆的左、右焦点分别为F1(-c,0),F2(c,0),
过F2且与x轴垂直的直线交C于A,B.
由e=
,得
=
,即c=
a,
结合b2=a2-c2,得b2=
a2.
因为S四边形AF1BC=S△AF1C+S△BF1C=2S△AF1C,
由S四边形AF1BC=
+4,得2•
•(a+c)•
=
+4,
即(a+
a)•
=
+4,解得a2=20,
从而b2=
×20=4,
故椭圆C的方程为
+
=1.
(2)由直线l过点B(-2,0),可设l:x=my-2,
又设点M(x1,y1),N(x2,y2),P(x3,y3),Q(x4,y4),
联立l与圆的方程,消去x,整理,得(m2+1)y2-4my-4=0,
由韦达定理,得
,且△1>0,
则|MN|=
•
=
•
=4•
,
由|MN|∈[4,2
],解得0≤m2≤3.
联立
,消去x,整理,得(m2+5)y2-4my-16=0,
由韦达定理,得
,且△2>0,
则|PQ|=
•
=
•
,
又原点O到直线l的距离d=
,
所以S△POQ=
|PQ|•d=4
•
=4
•
,
令
=t,则S△POQ=4
•
,
由0≤m2≤3,得
≤t≤
,所以
≤S△POQ≤
,
故△OPQ面积的取值范围是[
,
].
过F2且与x轴垂直的直线交C于A,B.
由e=
2
| ||
| 5 |
| c |
| a |
| 2 | ||
|
| 2 | ||
|
结合b2=a2-c2,得b2=
| 1 |
| 5 |
因为S四边形AF1BC=S△AF1C+S△BF1C=2S△AF1C,
由S四边形AF1BC=
8
| ||
| 5 |
| 1 |
| 2 |
| b2 |
| a |
8
| ||
| 5 |
即(a+
| 2 | ||
|
| ||
| a |
8
| ||
| 5 |
从而b2=
| 1 |
| 5 |
故椭圆C的方程为
| x2 |
| 20 |
| y2 |
| 4 |
(2)由直线l过点B(-2,0),可设l:x=my-2,
又设点M(x1,y1),N(x2,y2),P(x3,y3),Q(x4,y4),
联立l与圆的方程,消去x,整理,得(m2+1)y2-4my-4=0,
由韦达定理,得
|
则|MN|=
| m2+1 |
| (y1+y2)2-4y1y2 |
=
| m2+1 |
(
|
|
由|MN|∈[4,2
| 7 |
联立
|
由韦达定理,得
|
则|PQ|=
| m2+1 |
| (y3+y4)2-4y3y4 |
| m2+1 |
|
又原点O到直线l的距离d=
| 2 | ||
|
所以S△POQ=
| 1 |
| 2 |
| 5 |
|
| 5 |
-
|
令
| 1 |
| m2+5 |
| 5 |
-(t-
|
由0≤m2≤3,得
| 1 |
| 8 |
| 1 |
| 5 |
| ||
| 2 |
8
| ||
| 5 |
故△OPQ面积的取值范围是[
| ||
| 2 |
8
| ||
| 5 |
点评:1.本题考查了椭圆方程的求法,直线与圆的相交关系及直线与椭圆的相交关系等,综合性较强,关键是利用韦达定理表示弦长与三角形的面积.
2.要确定椭圆的标准方程,除了条件“c2=a2-b2”外,还需另外两个独立的条件,求解时应善于根据图形的几何性质或特征寻找关于a,b,c的等量关系.
3.对于三角形面积的取值范围或最值问题,一般是先引入参数,再用参数表示面积,转化为函数的值域问题求解.
2.要确定椭圆的标准方程,除了条件“c2=a2-b2”外,还需另外两个独立的条件,求解时应善于根据图形的几何性质或特征寻找关于a,b,c的等量关系.
3.对于三角形面积的取值范围或最值问题,一般是先引入参数,再用参数表示面积,转化为函数的值域问题求解.

练习册系列答案
相关题目
已知
=(1,
,3),
=(
,1,1),且
,
均在平面α内,直线l的方向向量
=(
,0,1),则( )
| a |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| a |
| b |
| υ |
| 1 |
| 2 |
| A、l?α | B、l与α相交 |
| C、l∥α | D、l?α或l∥α |
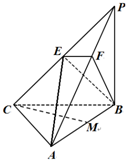 在三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,E为PC的中点,M为AB的中点,点F在PA上,且AF=2FP.
在三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,E为PC的中点,M为AB的中点,点F在PA上,且AF=2FP.