题目内容
13.设函数f(x)=aex+b,g(x)=x2+cx+d,若曲线y=f(x)和曲线y=g(x)都过点P(0,$\frac{1}{e}$),且在点P处有相同的切线y=$\frac{1}{e}$x+$\frac{1}{e}$.(1)求a,b,c,d的值;
(2)若函数h(x)=f(-|x|+1)-g(x+t)(t>0)存在零点,求证:0<t≤1.
分析 (1)由题意可得f(0)=g(0)=$\frac{1}{e}$,f′(0)=g′(0)=a=c=$\frac{1}{e}$,即可解得a,b,c,d的值;
(2)由函数h(x)存在零点,可得y=e-|x|和y=(x+t+$\frac{1}{2e}$)2+$\frac{4e-1}{4{e}^{2}}$的图象有交点,作出y=e-|x|和y=(x+$\frac{1}{2e}$)2+$\frac{4e-1}{4{e}^{2}}$的图象,由图象平移和相切的性质,设出切点(m,em),(m<0),求得导数,可得m,t的方程,解得m=-1,t=1,即可得到t的范围.
解答 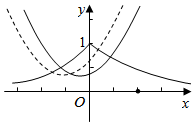 解:(1)由题意可得f(0)=g(0)=$\frac{1}{e}$,即为a+b=d=$\frac{1}{e}$,
解:(1)由题意可得f(0)=g(0)=$\frac{1}{e}$,即为a+b=d=$\frac{1}{e}$,
又f(x)的导数为f′(x)=aex,g(x)的导数为g′(x)=2x+c,
由题意可得f′(0)=g′(0)=a=c=$\frac{1}{e}$,
综上可得,a=$\frac{1}{e}$,b=0,c=$\frac{1}{e}$,d=$\frac{1}{e}$;
(2)证明:函数h(x)=f(-|x|+1)-g(x+t)
=e1-|x|-1-[(x+t)2+$\frac{1}{e}$(x+t)+$\frac{1}{e}$]=e-|x|-[(x+t+$\frac{1}{2e}$)2+$\frac{4e-1}{4{e}^{2}}$],
由函数h(x)存在零点,
可得y=e-|x|和y=(x+t+$\frac{1}{2e}$)2+$\frac{4e-1}{4{e}^{2}}$的图象有交点,
作出y=e-|x|和y=(x+$\frac{1}{2e}$)2+$\frac{4e-1}{4{e}^{2}}$的图象,
由t>0可得将抛物线的图象向左平移可得y=(x+t+$\frac{1}{2e}$)2+$\frac{4e-1}{4{e}^{2}}$的图象,
当图象经过点(0,1)时,1=(t+$\frac{1}{2e}$)2+$\frac{4e-1}{4{e}^{2}}$,解得t=1-$\frac{1}{e}$,
当抛物线的图象与y=e-|x|的图象相切时,设切点为(m,em),(m<0),
由切线的斜率相等,可得em=2(m+t+$\frac{1}{2e}$),
且em=(m+t+$\frac{1}{2e}$)2+$\frac{4e-1}{4{e}^{2}}$,解得m=-1,t=1,
则t的范围是0<t≤1.
点评 本题考查导数的运用:求切线的斜率,考查函数的零点问题的解法,注意运用图象转化为求交点问题,考查化简整理的运算能力,属于中档题.

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案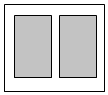 现需设计2016年春季湖北省重点高中联考协作体期中考试数学试卷,该试卷含有大小相等的左右相等两个矩形栏目(即图中阴影部分),这两栏的面积之和为720cm2,四周空白的宽度为4cm,两栏之间的中缝空白的宽度为2cm,设试卷的高和宽分别为xcm,ycm.
现需设计2016年春季湖北省重点高中联考协作体期中考试数学试卷,该试卷含有大小相等的左右相等两个矩形栏目(即图中阴影部分),这两栏的面积之和为720cm2,四周空白的宽度为4cm,两栏之间的中缝空白的宽度为2cm,设试卷的高和宽分别为xcm,ycm.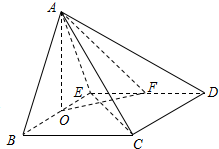 在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点.
在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点.