题目内容
8.已知sinx+cosx=a(0$≤a≤\sqrt{2}$),则sinnx+cosnx=($\frac{a+\sqrt{2-{a}^{2}}}{2}$)n+($\frac{a-\sqrt{2-{a}^{2}}}{2}$)n(关于a的表达式).分析 由sinx+cosx=a①,平方可得2sinxcosx=a2-1,可求sinx-cosx=±$\sqrt{2-{a}^{2}}$②,联立①②解得:sinx,cox,代入即可求值得解.
解答 解:∵sinx+cosx=a①,平方可得:1+2sinxcosx=a2,解得:2sinxcosx=a2-1,
∵0$≤a≤\sqrt{2}$,
∴0≤a2≤2,
∴sinx-cosx=±$\sqrt{1-2sinxcosx}$=±$\sqrt{2-{a}^{2}}$②,
∴联立①②解得:$\left\{\begin{array}{l}{sinx=\frac{a+\sqrt{2-{a}^{2}}}{2}}\\{cosx=\frac{a-\sqrt{2-{a}^{2}}}{2}}\end{array}\right.$,或$\left\{\begin{array}{l}{sinx=\frac{a-\sqrt{2-{a}^{2}}}{2}}\\{cosx=\frac{a+\sqrt{2-{a}^{2}}}{2}}\end{array}\right.$,
∴f(x)=sinnx+cosnx=($\frac{a+\sqrt{2-{a}^{2}}}{2}$)n+($\frac{a-\sqrt{2-{a}^{2}}}{2}$)n.
故答案为:($\frac{a+\sqrt{2-{a}^{2}}}{2}$)n+($\frac{a-\sqrt{2-{a}^{2}}}{2}$)n.
点评 本题主要考查了平方和公式,平方差公式的应用,考查了同角三角函数基本关系式的应用,属于基础题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
17.若函数f(x)满足f(x+1)=x2-x+2,则f(-1)=( )
| A. | 8 | B. | 5 | C. | 4 | D. | 3 |
18.1~100中所有奇数的和为( )
| A. | 99 | B. | 1250 | C. | 2500 | D. | 2525 |
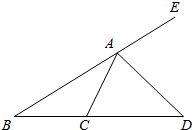 如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗?
如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗?