题目内容
11.一质点按规律s=2t3运动,则在t=2时的瞬时速度为24.分析 求质点在t=2时的瞬时速度,可以求出位移的导数,再将t=2代入既得;
解答 解:s=2t3,
s′=6t2,
在t=2时的瞬时速度为6×4=24.
故答案为:24.
点评 题考查的知识点是变化的快慢与变化率,其中根据质点位移与时间的关系时,求导得到质点瞬时速度的表达式是解答本题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
2.若a>b>c,则下列不等式中正确的是( )
| A. | ac>bc | B. | a-b>b-c | C. | a-c>b-c | D. | a+c>b |
16.已知函数f(x)是在定义域内最小正周期为π的奇函数,且在区间(0,$\frac{π}{2}$)是减函数,那么函数f(x)可能是( )
| A. | f(x)=sin2x | B. | f(x)=2tan$\frac{1}{2}$x | C. | f(x)=-tanx | D. | f(x)=sin($\frac{π}{2}$+2x) |
3.已知函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+4π)=f(x)+f(2π)成立,那么函数f(x)可能是( )
| A. | f(x)=2sin$\frac{1}{2}$x | B. | f(x)=2cos2$\frac{1}{4}$x | C. | f(x)=2cos2$\frac{1}{2}$x | D. | f(x)=2cos$\frac{1}{2}$x |
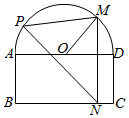 如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动.
如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动.