题目内容
12.在公差d不为零的等差数列{an}中,若a1=2,且a3是a1,a9的等比中项.(1)求数列{an}的通项公式;
(2)求数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前n项和Tn.
分析 (1)利用等比中项可${{a}_{3}}^{2}$=a1•a9,结合a1=2解方程可知公差d=2,进而计算可得结论;
(2)通过(1)裂项可知$\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{{2n•({2n+2})}}=\frac{1}{4}({\frac{1}{n}-\frac{1}{n+1}})$,进而并项相加即得结论.
解答 解:(1)∵a3是a1,a9的等比中项,{an}是等比数列,
∴${{a}_{3}}^{2}$=a1•a9,即$({a}_{1}+2d)^{2}$=a1(a1+8d),
又∵a1=2,
∴(2+2d)2=2•(2+8d),
化简得:d2-2d=0,
又∵d≠0,
∴d=2,
∴an=2n;
(2)由(1)可知$\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{{2n•({2n+2})}}=\frac{1}{4}({\frac{1}{n}-\frac{1}{n+1}})$,
∴${T_n}=\frac{1}{4}({1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…\frac{1}{n}-\frac{1}{n+1}})=\frac{1}{4}({1-\frac{1}{n+1}})=\frac{n}{{4({n+1})}}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
6.在射击试验中,令X=$\left\{\begin{array}{l}{1,射中}\\{0,未射中}\end{array}\right.$如果射中的概率是0.9,则随机变量的分布列为
.
| X | 0 | 1 |
| P | 0.1 | 0.9 |
4.方程sinx=-$\frac{1}{2}$的解为( )
| A. | x=kπ+(-1)k•$\frac{π}{6}$,k∈Z | B. | x=2kπ+(-1)k•$\frac{π}{6}$,k∈Z | ||
| C. | x=kπ+(-1)k+1•$\frac{π}{6}$,k∈Z | D. | x=2kπ+(-1)k+1•$\frac{π}{6}$,k∈Z |
2.若a>b>c,则下列不等式中正确的是( )
| A. | ac>bc | B. | a-b>b-c | C. | a-c>b-c | D. | a+c>b |
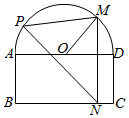 如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动.
如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动.