题目内容
16．在等差数列{an}中，已知${a_3}=-2，{a_n}=\frac{3}{2}，{S_n}=-\frac{15}{2}$，则a1=-3或$-\frac{19}{6}$．分析 利用等差数列的通项公式及其前n项和公式即可得出．
解答 解：设等差数列{an}的公差为d，∵${a_3}=-2，{a_n}=\frac{3}{2}，{S_n}=-\frac{15}{2}$，
∴a1+2d=-2，a1+（n-1）d=$\frac{3}{2}$，$\frac{n（{a}_{1}+\frac{3}{2}）}{2}$=-$\frac{15}{2}$，
解得a1=-3或$-\frac{19}{6}$，
故答案为：-3或$-\frac{19}{6}$；
点评 本题考查了等差数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
考前必练系列答案
相关题目
4．方程sinx=-$\frac{1}{2}$的解为（ ）
| A． | x=kπ+（-1）k•$\frac{π}{6}$，k∈Z | B． | x=2kπ+（-1）k•$\frac{π}{6}$，k∈Z | ||
| C． | x=kπ+（-1）k+1•$\frac{π}{6}$，k∈Z | D． | x=2kπ+（-1）k+1•$\frac{π}{6}$，k∈Z |
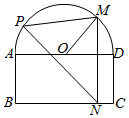如图，一个半圆和长方形组成的铁皮，长方形的边AD为半圆的直径，O为半圆的圆心，AB=2，BC=4，现要将此铁皮剪出一个△PMN，其中边MN⊥BC，点P在曲线MAB上运动．