题目内容
20．6张同排连号的电影票，分给3名教师与3名学生，若要求师生相间而坐，则不同的分法有（ ）| A． | $A_3^3$•$A_4^3$ | B． | $A_3^3$•$A_3^3$ | C． | $A_4^3$•$A_4^3$ | D． | 2$A_3^3$•$A_3^3$ |
分析 可用插空法求解此题，先排三个学生，有A33种排法，再把3名教师插入1，2，3空或2，3，4空，有2A33种坐法．由分步原理计数即可．
解答 解：由题意不同的安排方法可以分为两步来解决，第一步先排三位学生有A33种排法；
第二步把3名教师插入1，2，3空或2，3，4空，有2A33种坐法；
故不同的分法种数有2A33×A33种．
故选：D．
点评 本题考查排列知识的运用，考查插空法，考查学生分析解决问题的能力，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．命题“若x2＜9，则-3＜x＜3”的逆否命题是（ ）
| A． | 若x2≥9，则x≥3或x≤-3 | B． | 若-3＜x＜3，则x2＜9 | ||
| C． | 若x＞3或x＜-3，则x2＞9 | D． | 若x≥3或x≤-3，则x2≥9 |
15．过点A（-4，0）向椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）引两条切线，切点分别为B、C，若△ABC为正三角形，则当ab最大时椭圆的方程为（ ）
| A． | $\frac{{x}^{2}}{8}$+$\frac{3{y}^{2}}{8}$=1 | B． | $\frac{{x}^{2}}{16}$+$\frac{3{y}^{2}}{16}$=1 | C． | $\frac{{x}^{2}}{9}$+$\frac{4{y}^{2}}{9}$=1 | D． | $\frac{{x}^{2}}{9}$+$\frac{8{y}^{2}}{9}$=1 |
5．观察下列各式：55=3 125，56=15 625，57=78 125，…，则52011的末四位数字为（ ）
| A． | 3 125 | B． | 5 625 | C． | 0 625 | D． | 8 125 |
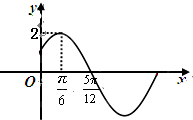已知函数f（x）=Asin（ωx+φ）（φ|＜$\frac{π}{2}$）的部分图象如图所示．