题目内容
已知函数f(x)=2x且f(x)=g(x)+h(x),其中g(x)为奇函数,h(x)为偶函数,若不等式2a•g(x)+h(2x)≥0对任意x∈[1,2]恒成立,则
(1)g(x)= .
(2)实数a的取值范围是 .
(1)g(x)=
(2)实数a的取值范围是
考点:指数函数综合题
专题:函数的性质及应用
分析:(1)根据函数奇偶性的性质建立方程组即可求出g(x)的表达式.
(2)根据指数函数的性质,利用换元法将不等式恒成立转化为参数恒成立问题,利用基本不等式的性质即可得到结论.
(2)根据指数函数的性质,利用换元法将不等式恒成立转化为参数恒成立问题,利用基本不等式的性质即可得到结论.
解答:
解:(1)∵f(x)=g(x)+h(x),其中g(x)为奇函数,h(x)为偶函数,
∴f(-x)=g(-x)+h(-x)=-g(x)+h(x),
两式联立得g(x)=
=
.
(2)若不等式2a•g(x)+h(2x)≥0对任意x∈[1,2]恒成立,
即a(2x-2-x)+
≥0恒成立,
令t=2x-2-x,
则t∈[
,
],
则22x+2-2x=(2x-2-x)2+2=t2+2,
即2at+t2+2≥0在t∈[
,
]上恒成立,
即a≥-
(t+
)恒成立,
∵y=t+
在t∈[
,
]上单调递增,
∴当t=
时,t+
取得最小值为
,
∴-
(t+
)的最大值为-
,
∴a≥-
.
故答案为:(1)
,(2)a≥-
.
∴f(-x)=g(-x)+h(-x)=-g(x)+h(x),
两式联立得g(x)=
| f(x)-f(-x) |
| 2 |
| 2x-2-x |
| 2 |
(2)若不等式2a•g(x)+h(2x)≥0对任意x∈[1,2]恒成立,
即a(2x-2-x)+
| 22x+2-2x |
| 2 |
令t=2x-2-x,
则t∈[
| 3 |
| 2 |
| 15 |
| 4 |
则22x+2-2x=(2x-2-x)2+2=t2+2,
即2at+t2+2≥0在t∈[
| 3 |
| 2 |
| 15 |
| 4 |
即a≥-
| 1 |
| 2 |
| 2 |
| t |
∵y=t+
| 2 |
| t |
| 3 |
| 2 |
| 15 |
| 4 |
∴当t=
| 3 |
| 2 |
| 2 |
| t |
| 17 |
| 6 |
∴-
| 1 |
| 2 |
| 2 |
| t |
| 17 |
| 12 |
∴a≥-
| 17 |
| 12 |
故答案为:(1)
| 2x-2-x |
| 2 |
| 17 |
| 12 |
点评:本题主要考查函数奇偶性的应用,以及不等式恒成立问题,将不等式恒成立进行转化,利用参数分离法是解决本题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
实数x,y满足
,则目标函数z=2x-y的最大值为( )
|
| A、4 | B、3 | C、0 | D、-1 |

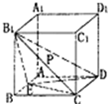 如图,正方体ABCD-A1B1C1D1的棱长为1,E是AB的中点,P是B1C的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E是AB的中点,P是B1C的中点.