题目内容
13.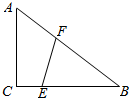 如图,在△ABC中,∠C=90°,AC=3,BC=4,AB边(包括端点)上一点F,BC边(包括端点)上一点E满足线段EF分△ABC的面积为相等的两部分;
如图,在△ABC中,∠C=90°,AC=3,BC=4,AB边(包括端点)上一点F,BC边(包括端点)上一点E满足线段EF分△ABC的面积为相等的两部分;(1)设BF=x,EF=y,将y表示为x的函数;
(2)求线段EF长的取值范围.
分析 (1)过F作FG⊥BE于G,把sinB用含有x的代数式表示,得到FG=$\frac{3}{5}x,BG=\frac{4}{5}x$,进一步得到EG,然后利用等积法列式可得$y=\sqrt{{x}^{2}+\frac{100}{{x}^{2}}-16}$($\frac{5}{2}≤$x≤5);
(2)利用函数的单调性求得线段EF长的取值范围.
解答 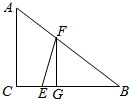 解:(1)设BF=x,EF=y,
解:(1)设BF=x,EF=y,
∵∠C=90°,AC=3,BC=4,∴AB=5,
过F作FG⊥BE于G,则$sinB=\frac{3}{5}$=$\frac{FG}{x}$,
∴FG=$\frac{3}{5}x$,BG=$\frac{4}{5}x$,
则EG=$\sqrt{{y^2}-\frac{9}{25}{x^2}}$,
故有$\frac{1}{2}(\sqrt{{y^2}-\frac{9}{25}{x^2}}+\frac{4}{5}x)\frac{3}{5}x=\frac{1}{2}×\frac{1}{2}×3×4$.
化简,得:${y^2}={x^2}+\frac{100}{x^2}-16$($\frac{5}{2}$≤x≤5).
∴$y=\sqrt{{x}^{2}+\frac{100}{{x}^{2}}-16}$($\frac{5}{2}≤$x≤5);
(2)设f(x)=${y^2}={x^2}+\frac{100}{x^2}-16$($\frac{5}{2}$≤x≤5).
∵f(x)在[$\frac{5}{2},\sqrt{10}$]上为减函数,在($\sqrt{10},5$]上为增函数,
且f($\frac{5}{2}$)=$\frac{25}{4}$,f(5)=13,f($\sqrt{10}$)=4,
∴线段WF长的取值范围为$[2,\sqrt{13}]$.
点评 本题考查函数解析式的求解及常用方法,考查简单的数学建模思想方法,是中档题.

 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案| A. | 2 | B. | 1 | C. | 3 | D. | $\frac{9}{4}$ |
| A. | x2+x | B. | -x2+x | C. | -x2-x | D. | x2-x |
| A. | 3=M | B. | a+1=M | C. | M-1=a | D. | M=a+1 |
| A. | 当x>0且x≠1时,lgx+$\frac{1}{lgx}$≥2 | |
| B. | 当x>0时,$\sqrt{x}+\frac{1}{{\sqrt{x}}}$≥2 | |
| C. | 当x≥2时,x+$\frac{1}{x}$的最小值为2 | |
| D. | 当$x∈(0,\frac{π}{2}]$时,f(x)=sinx+$\frac{4}{sinx}$的最小值是4 |