题目内容
18．已知$sinα=\frac{4}{5}$，并且α是第二象限，求cosα，tanα的值．分析 利用同角三角函数关系式求解．
解答 解：∵$sinα=\frac{4}{5}$，且α是第二象限，
∴cosα=-$\sqrt{1-（\frac{4}{5}）^{2}}$=-$\frac{3}{5}$，
tanα=$\frac{sinα}{cosα}$=$\frac{\frac{4}{5}}{-\frac{3}{5}}$=-$\frac{4}{3}$．
点评 本题考查三角函数值的求法，是基础题，解题时要认真审题，注意三角函数性质的合理运用．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
8．如图是一个空间几何体的三视图，则该几何体的体积是（ ）
| A． | 4-4π | B． | 8-$\frac{2π}{3}$ | C． | 4-2π | D． | 4-$\frac{2π}{3}$ |
9．一个几何体的三视图如图所示，则这个几何体的外接球的体积为（ ）
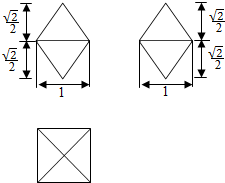
| A． | $\frac{{\sqrt{2}}}{3}π$? | B． | $\sqrt{2}π$? | C． | 2π? | D． | $\frac{{2\sqrt{2}}}{3}π$? |
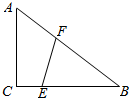如图，在△ABC中，∠C=90°，AC=3，BC=4，AB边（包括端点）上一点F，BC边（包括端点）上一点E满足线段EF分△ABC的面积为相等的两部分；
10．条件p：|x+1|＞1，条件$q：\frac{1}{3-x}＞1$，则￢q是￢p的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |