题目内容
2.下列结论正确的是( )| A. | 当x>0且x≠1时,lgx+$\frac{1}{lgx}$≥2 | |
| B. | 当x>0时,$\sqrt{x}+\frac{1}{{\sqrt{x}}}$≥2 | |
| C. | 当x≥2时,x+$\frac{1}{x}$的最小值为2 | |
| D. | 当$x∈(0,\frac{π}{2}]$时,f(x)=sinx+$\frac{4}{sinx}$的最小值是4 |
分析 本题中各选项都是利用基本不等式求最值,注意验证一正、二定、三相等条件是否满足即可.A中不满足“正数”,C、D中“=”取不到
解答 解:解:A中,当0<x<1时,lgx<0,lgx+$\frac{1}{lgx}$≥2不成立;由基本不等式B正确;
C中“=”取不到;D中等号取不到,
故选B.
点评 本题主要考查利用基本不等式求最值的三个条件,一正、二定、三相等,在解题中要牢记

练习册系列答案
相关题目
10.条件p:|x+1|>1,条件$q:\frac{1}{3-x}>1$,则¬q是¬p的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
17.已知数列{an}的前n项和为Sn,a1=1,Sn=3an+1-3,则an=( )
| A. | ${({\frac{4}{3}})^{n-1}}$ | B. | ${({\frac{3}{4}})^{n-1}}$ | C. | 3n-1 | D. | ${({\frac{1}{3}})^{n-1}}$ |
14.若函数f(x)=ax-1+1(a>0且a≠1)的反函数恒过定点( )
| A. | (0,2) | B. | (2,0) | C. | (1,2) | D. | (2,1) |
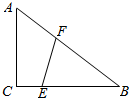 如图,在△ABC中,∠C=90°,AC=3,BC=4,AB边(包括端点)上一点F,BC边(包括端点)上一点E满足线段EF分△ABC的面积为相等的两部分;
如图,在△ABC中,∠C=90°,AC=3,BC=4,AB边(包括端点)上一点F,BC边(包括端点)上一点E满足线段EF分△ABC的面积为相等的两部分;