题目内容
3.若x=1是函数f(x)=$\frac{1}{3}$m2x3+mx2+nx+p的一个极值点,则n的最大值为( )| A. | 2 | B. | 1 | C. | 3 | D. | $\frac{9}{4}$ |
分析 求出函数的导数,利用函数的极值点,列出方程然后利用二次函数求解最值.
解答 解:函数f(x)=$\frac{1}{3}$m2x3+mx2+nx+p,
可得f′(x)=m2x2+2mx+n,
x=1是函数f(x)=$\frac{1}{3}$m2x3+mx2+nx+p的一个极值点,
可得m2+2m+n=0,
即n=-m2-2m=-(m+1)2+1≤1.
n的最大值为:1.
故选:B.
点评 本题考查函数的极值的求法二次函数的简单性质的应用,考查分析问题解决问题的能力,转化思想的应用.

练习册系列答案
相关题目
8.如图是一个空间几何体的三视图,则该几何体的体积是( )


| A. | 4-4π | B. | 8-$\frac{2π}{3}$ | C. | 4-2π | D. | 4-$\frac{2π}{3}$ |
 ,
,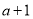 ,
,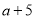 成等比数列,其倒数重新排列后为递增的等比数列
成等比数列,其倒数重新排列后为递增的等比数列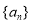 的前三项,则能使不等式
的前三项,则能使不等式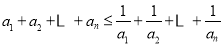 成立的自然数
成立的自然数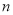 的最大值为( )
的最大值为( ) ,
, ,
, ,若
,若 为实数,
为实数, ,则
,则 ( )
( ) B.
B. C.1 D.2
C.1 D.2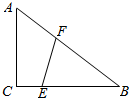 如图,在△ABC中,∠C=90°,AC=3,BC=4,AB边(包括端点)上一点F,BC边(包括端点)上一点E满足线段EF分△ABC的面积为相等的两部分;
如图,在△ABC中,∠C=90°,AC=3,BC=4,AB边(包括端点)上一点F,BC边(包括端点)上一点E满足线段EF分△ABC的面积为相等的两部分;