Question

已知函数f(x)＝ln x－.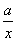

(1)若a>0，试判断f(x)在定义域内的单调性；

(2)若f(x)<x²在(1，＋∞)上恒成立，求a的取值范围．

Answer 1

解：(1)由题意知f(x)的定义域为(0，＋∞)，

且f′(x)＝＋＝.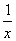

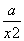∵a>0，∴f′(x)>0，

故f(x)在(0，＋∞)上是单调递增函数．

(2)∵f(x)<x²，∴ln x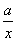－<x².

又x>0，∴a>xln x－x³.

令g(x)＝xln x－x³，

h(x)＝g′(x)＝1＋ln x－3x²，

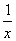h′(x)＝－6x＝.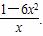

∵x∈(1，＋∞)时，h′(x)<0，

∴h(x)在(1，＋∞)上是减函数．

∴h(x)<h(1)＝－2<0，即g′(x)<0，

∴g(x)在(1，＋∞)上也是减函数．

g(x)<g(1)＝－1，∴当a≥－1时，f(x)<x²在(1，＋∞)上恒成立．