题目内容
已知复数z2=2cosθ+(λ+3sinθ)i,z1=m+(4-m2)i(m∈R),(λ,θ∈R)并且z1=z2,则λ的取值范围 .
考点:复数代数形式的乘除运算
专题:计算题,数系的扩充和复数
分析:由z1=z2,得
,消掉m得λ=4-4cos2θ-3sinθ=4sin2θ-3sinθ,借助二次函数的性质可求λ的取值范围.
|
解答:
解:∵z1=z2,
∴
,消掉m,得
λ=4-4cos2θ-3sinθ=4sin2θ-3sinθ=4(sinθ-
)2-
,
又-1≤sinθ≤1,
∴sinθ=
时,λmin=-
;sinθ=-1时,λmax=7.
∴λ的取值范围是[-
,7],
故答案为:[-
,7].
∴
|
λ=4-4cos2θ-3sinθ=4sin2θ-3sinθ=4(sinθ-
| 3 |
| 8 |
| 9 |
| 16 |
又-1≤sinθ≤1,
∴sinθ=
| 3 |
| 8 |
| 9 |
| 16 |
∴λ的取值范围是[-
| 9 |
| 16 |
故答案为:[-
| 9 |
| 16 |
点评:该题考查复数相等的充要条件、三角恒等变换及二次函数的性质等知识,属基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
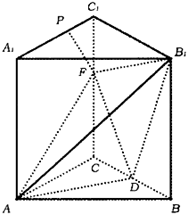 在直三棱柱ABC-A1B1C1中,AB=AC═3,BC=2,D是BC的中点,F是上一点,且CF=2.
在直三棱柱ABC-A1B1C1中,AB=AC═3,BC=2,D是BC的中点,F是上一点,且CF=2.