题目内容
16.用定积分的几何意义求下列各式的值.(1)${∫}_{-1}^{1}$$\sqrt{4-{x}^{2}}$dx;
(2)${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$sinxdx.
分析 由定积分的几何意义可得
(1)${∫}_{-1}^{1}$$\sqrt{4-{x}^{2}}$dx表示圆x2+y2=4的圆x2+y2=4的在[-1,1]上圆的面积;
(2)${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$sinxdx表示正弦曲线和x轴在[-$\frac{π}{2}$,$\frac{π}{2}$]面积的代数和,由奇函数图象的对称性可得.
解答 解:(1)由y=$\sqrt{4-{x}^{2}}$可得x2+y2=4,
∴${∫}_{-1}^{1}$$\sqrt{4-{x}^{2}}$dx表示圆x2+y2=4的在[-1,1]上圆的面积
故${∫}_{-1}^{1}$$\sqrt{4-{x}^{2}}$dx=4π-($\frac{2×4π}{3}$-2×$\frac{1}{2}$×1×$\sqrt{3}$)=$\frac{4π}{3}$+$\sqrt{3}$;
(2)同理由定积分的意义可知${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$sinxdx表示
正弦曲线和x轴在[-$\frac{π}{2}$,$\frac{π}{2}$]面积的代数和,
由奇函数图象的对称性可得${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$sinxdx=0
点评 本题考查定积分的几何意义,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.下列条件中,能判断两个平面平行的是( )
| A. | 一个平面内有无数条直线平行于另一个平面 | |
| B. | 一个平面内有两条直线平行于另一个平面 | |
| C. | 一个平面内有两条相交直线平行于另一个平面 | |
| D. | 两个平面同时垂直于另一个平面 |
1.如图所示,在正面体ABCD-A1B1C1D1中,AD1∩A1D=O,则线段CO在平面AD1内的射影是( )
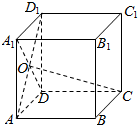

| A. | 线段DO | B. | 线段D1O | C. | 线段A1O | D. | 线段AO |
8.若复数z满足z(6-8i)=|8+6i|(i是虚数单位),则z的虚部为( )
| A. | $\frac{4}{5}$ | B. | 4 | C. | -$\frac{4}{5}$ | D. | -4 |