题目内容
求(
+
)8的展开式中二项式系数最大项．
| x |
| 1 | |||
|
考点：二项式系数的性质
专题：二项式定理
分析：由于(
+
)8的展开式共有9项，故展开式中二项式系数最大项是第5项，再根据通项公式求出第5项．
| x |
| 1 | |||
|
解答：
解：由于(
+
)8的展开式共有9项，故展开式中二项式系数最大项是第5项，
即 T5=T4+1=
(
)4(
)4=70x
．
| x |
| 1 | |||
|
即 T5=T4+1=
| C | 4 8 |
| x |
| 1 | |||
|
| 2 |
| 3 |
点评：本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知点A、B、C为椭圆
+y2=1上三点，其中A（1，
），且△ABC的内切圆圆心在直线x=1上，则△ABC三边斜率和为（ ）
| x2 |
| 4 |
| ||
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
棱长为a的正方体内切一球，该球的表面积为（ ）
| A、πa2 |
| B、2πa2 |
| C、3πa2 |
| D、4πa2 |
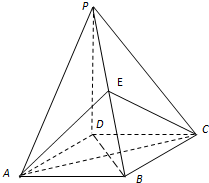如图，四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上．
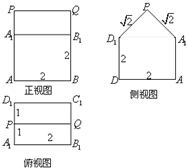某一几何体的三视图如图所示．按照给出的尺寸（单位：cm）：