题目内容
16.已知函数f(x)=x2-2(a-1)x+2在区间(-∞,5]上为减函数,则实数a的取值范围为[6,+∞).分析 由函数f(x)=x2-2(a-1)x+2的解析式,根据二次函数的性质,判断出其图象是开口方向朝上,以x=a-1为对称轴的抛物线,此时在对称轴左侧的区间为函数的递减区间,由此可构造一个关于a的不等式,解不等式即可得到实数a的取值范围.
解答 解:函数f(x)=x2-2(a-1)x+2的图象是开口方向朝上,
以x=a-1为对称轴的抛物线,
若函数f(x)=x2-2(a-1)x+2在区间(-∞,5]上是减函数,
则a-1≥5,
解得a≥6.
故答案为:[6,+∞).
点评 本题考查的知识点是函数单调性的性质,及二次函数的性质,其中根据已知中函数的解析式,分析出函数的图象形状,进而分析函数的单调性,是解答此类问题最常用的办法.

练习册系列答案
相关题目
1.某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
(Ⅰ)写出价格f(x)关于时间x的函数关系式(x表示投放市场的第x天,x∈N*);
(Ⅱ)销售量g(x)与时间x的函数关系式为$g(x)=-\frac{1}{3}x+\frac{109}{3}({1≤x≤100,x∈{N^*}})$,则该产品投放市场第几天的销售额最高?最高为多少千元?
| 时间 | 第4天 | 第32天 | 第60天 | 第90天 |
| 价格(千元) | 23 | 30 | 22 | 7 |
(Ⅱ)销售量g(x)与时间x的函数关系式为$g(x)=-\frac{1}{3}x+\frac{109}{3}({1≤x≤100,x∈{N^*}})$,则该产品投放市场第几天的销售额最高?最高为多少千元?
8.某地区教学考试的成绩X~N(100,100),成绩X位于区间(110,120]的概率是( )
参考数据
P(μ-σ<X≤μ+σ)=0.6826
P(μ-2σ<X≤μ+2σ)=0.9544
P(μ-3σ<X≤μ+3σ)=0.9974.
参考数据
P(μ-σ<X≤μ+σ)=0.6826
P(μ-2σ<X≤μ+2σ)=0.9544
P(μ-3σ<X≤μ+3σ)=0.9974.
| A. | 0.6826 | B. | 0.9544 | C. | 0.2718 | D. | 0.1359 |
5.已知等差数列{an}满足a1=2,a3=8,则数列{an}的公差为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.把2名新生分到甲、乙、丙、丁四个班,甲班必须且只能分配1名新生,则不同的分配方法有( )
| A. | 3种 | B. | 4种 | C. | 6种 | D. | 8种 |
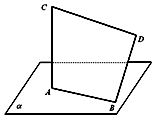 如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.
如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.