题目内容
7.△ABC中,角A,B,C的对边分别为a,b,c,若△ABC的面积S=(b+c)2-a2,则sinA=$\frac{8}{17}$.分析 由已知利用余弦定理,三角形面积公式可解得cosA=$\frac{1}{4}$sinA-1,两边平方结合sinA≠0,即可解得sinA的值.
解答 解:∵由余弦定理可得:b2+c2-a2=2bccosA,S=b2+c2-a2+2bc,
∴$\frac{1}{2}$bcsinA=2bc+2bccosA,
∴cosA=$\frac{1}{4}$sinA-1,两边平方,整理可得:$\frac{17si{n}^{2}A}{8}$=sinA,
∵A为三角形内角,sinA≠0,
∴解得:sinA=$\frac{8}{17}$.
故答案为:$\frac{8}{17}$.
点评 本题主要考查了余弦定理,三角形面积公式,同角三角函数基本关系式的应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
16.某“帆板”集训队在一海滨区域进行集训,该海滨区域的海浪高度y(米)随着时间t(0≤t≤24,单位:小时)而周期性变化.每天各时刻t的浪高数据的平均值如下表:
(1)试在图中描出所给点;
(2)观察图,从y=at+b,y=Asin(ωt+φ)+b,y=Acos(ωt+φ)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定在一天内的7时至19时之间,当浪高不低于0.8米时才进行训练,试安排恰当的训练时间.
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.4 | 1.0 |
(2)观察图,从y=at+b,y=Asin(ωt+φ)+b,y=Acos(ωt+φ)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定在一天内的7时至19时之间,当浪高不低于0.8米时才进行训练,试安排恰当的训练时间.
17.2015年8月12日天津发生危化品重大爆炸事故,造成重大人员和经济损失.某港口组织消防人员对该港口的公司的集装箱进行安全抽检,已知消防安全等级共分为四个等级(一级为优,二级为良,三级为中等,四级为差),该港口消防安全等级的统计结果如下表所示:
现从该港口随机抽取了n家公司,其中消防安全等级为三级的恰有20家.
(1)求m,n的值;
(2)按消防安全等级利用分层抽样的方法从这n家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
| 等 级 | 一级 | 二级 | 三级 | 四级 |
| 频 率 | 0.30 | 2m | m | 0.10 |
(1)求m,n的值;
(2)按消防安全等级利用分层抽样的方法从这n家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
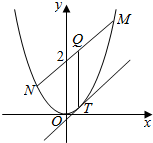 已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.
已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.