题目内容

3．在数列{an}中，已知an=$\frac{n}{n+1}$，则{an}是（　　）
A．递增数列B．递减数列C．常数列D．摆动数列

分析 作差an+1-an，判断符号即可得出．

解答 解：∵an+1-an=$\frac{n+1}{n+2}$-$\frac{n}{n+1}$=$\frac{1}{（n+1）（n+2）}$＞0，
∴an+1＞an．
∴{an}是单调递增数列，
故选：A．

点评 本题考查了数列的单调性，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
13．函数y=$\frac{{2}^{x}-1}{{2}^{x}+1}$的奇偶性为奇函数，函数f（x）=$\frac{2}{{2}^{x}+1}$+1的对称中心为（0，2）．
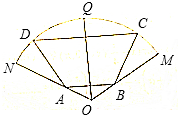14．如图，扇形MON的半径为2，圆心角为$\frac{2}{3}$π，四边形ABCD为扇形的内接等腰梯形，其中底边AB的两个端点分别在半径ON和0M上，C、D在弧$\widehat{MQN}$上，Q为弧$\widehat{MN}$的中点，∠ABC=$\frac{2}{3}$π，求梯形ABCD面积的最大值．
11．${C}_{4}^{1}$+${C}_{4}^{2}$+${C}_{4}^{3}$+${C}_{4}^{4}$=15．
18．已知函数g（x）=-$\frac{1}{2}$x2-x+2，x∈[a，a+1]，求g（x）的最大值h（a）．
8．设方程（x-k）2+（y-1）2=-k2+k+2表示圆，求实数k的取值范围．
15．己知平面向量|$\overrightarrow{OA}$|=2，$\overrightarrow{OA}$与$\overrightarrow{OB}$-$\overrightarrow{OA}$的夹角为120°，$\overrightarrow{OC}$=$λ\overrightarrow{OA}$+（1-λ）$\overrightarrow{OB}$（λ∈R），求|$\overrightarrow{OC}$|的最小值．
12．已知函数f（x）=x2+nx+m，若{x|f（x）=0}={x|f（f（x））=0}≠∅，则m+n的取值范围是[0，4）．
5．如图，四棱锥P-ABCD中，∠BAD=∠ABC=90°，BC=2AD，△PAB和△PAD都是等边三角形，则异面直线CD与PB所成角的大小为90°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网