题目内容

7．在等差数列{an}中，若a3+a4+a5+a6+a7=20，则a5=（　　）
A．10B．6C．5D．4

分析 根据等差数列的性质进行求解即可．

解答 解：在等差数列{an}中，若a3+a4+a5+a6+a7=20，
则5a5=20，
得a5=4，
故选：D．

点评 本题主要考查等差数列的性质，比较基础．

练习册系列答案
相关题目
17．已知x，y满足（x-1）2+y2=16，则x2+y2的最大值为（　　）
A．3B．5C．9D．25
18．已知数列{an}的前n项和Sn，a1=1，an≠0，且Sn=$\frac{1}{2}$anan+1（n∈N*）．
（1）求数列{an}的通项公式；
（2）记bn=$\frac{1}{{a}_{n}{a}_{n+1}{a}_{n+2}}$，设Tn为数列bn的前n项和，且Tn＜|x+m|+|x-3m|对任意实数x恒成立，求m的取值范围．
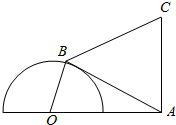15．如图，半圆O的直径为2，A为直径延长线上的一点，OA=2，B为半圆上任意一点，以AB为一边作等边三角形ABC，设∠AOB=α．问：当α取何值时，四边形OACB面积最大？
2．化简方程$\sqrt{（x-1）^{2}+{y}^{2}}$+$\sqrt{（x+1）^{2}+{y}^{2}}$=4为有理方程，其结果是$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$．
12．已知$\sqrt{2}$，a+1，2$\sqrt{2}$成等比数列，则a的值为（　　）
A．-3B．1C．-1或3D．-3或1
19．数列{（-1）n（2n-1）}的前2015项的和S2015=-1008．
16．${（x-\frac{1}{x}）^6}$展开式中的常数项为（　　）
A．15B．20C．-1D．-20
17．求证：
（1）如果a＞b，ab＞0，那么$\frac{1}{a}$＜$\frac{1}{b}$；
（2）如果a＞b＞0，c＜d＜0，那么ac＜bd．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网