题目内容
19.已知向量,$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(3,-2),且($\overrightarrow{a}$+$\overrightarrow{b}$)∥$\overrightarrow{b}$,则m=( )| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -8 | D. | 8 |
分析 称利用向量坐标运算法则求出$\overrightarrow{a}+\overrightarrow{b}$=(4,m-2),再由($\overrightarrow{a}$+$\overrightarrow{b}$)∥$\overrightarrow{b}$,利用向量平行的性质能求出m.
解答 解:∵$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(3,-2),
∴$\overrightarrow{a}+\overrightarrow{b}$=(4,m-2),
∵($\overrightarrow{a}$+$\overrightarrow{b}$)∥$\overrightarrow{b}$,
∴$\frac{4}{3}=\frac{m-2}{-2}$,
解得m=-$\frac{2}{3}$.
故选:A.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意向量平行的性质的合理运用.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
10.已知a=0.40.4,b=1.20.4,c=log20.4,则a,b,c的大小关系为( )
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | a<c<b |
7.已知命题p:?x0∈R,x0-2>0,命题q:?x∈R,$\sqrt{x}$<x,则下列说法中正确的是( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
11.已知集合M={x|x2-2x-8≤0},集合N={x|lgx≥0},则M∩N=( )
| A. | {x|x≥4} | B. | {x|1≤x≤4} | C. | {x|x≥1} | D. | {x|x≥-2} |
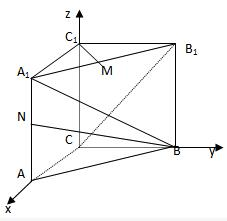 如图所示,直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图所示,直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.