题目内容
17.已知函数f(x)=x-$\frac{lnx}{m}$,m∈R,且m≠0.(1)讨论函数f(x)的单调性;
(2)若m=-1,求证:函数F(x)=x-$\frac{f(x)}{x}$有且只有一个零点.
分析 (1)求出原函数的导函数,然后分m<0和m>0两种情况讨论原函数的单调性;
(2)把m=-1代入函数解析式,求出导函数F′(x)=$\frac{{x}^{2}-1+lnx}{{x}^{2}}$,设h(x)=x2-1+lnx,利用导数可得h(x)=x2-1+lnx在(0,+∞)上为增函数,结合h(1)=0,可得F′(1)=0且F′(x)有唯一的零点1.从而得到0<x<1时,F′(x)<0,x>1时,F′(x)>0.可得F(x)在(0,1)上为减函数,在(1,+∞)上为增函数,结合F(x)的最小值为F(1)=0可知函数F(x)=x-$\frac{f(x)}{x}$有且只有一个零点.
解答 (1)解:f′(x)=1-$\frac{1}{mx}$=$\frac{mx-1}{mx}$,x>0,
当m<0时,f′(x)>0,则f(x)在(0,+∞)上单调递增;
当m>0时,由f′(x)>0,解得x>$\frac{1}{m}$,由f′(x)<0,得0<x<$\frac{1}{m}$.
∴f(x)在区间(0,$\frac{1}{m}$)上单调递减,在($\frac{1}{m}$,+∞)上单调递增;
(2)证明:由已知,F(x)=x-$\frac{lnx}{x}-1$,则F′(x)=$\frac{{x}^{2}-1+lnx}{{x}^{2}}$,
设h(x)=x2-1+lnx,则h′(x)=2x+$\frac{1}{x}$>0(x>0),
故h(x)=x2-1+lnx在(0,+∞)上为增函数,
又由于h(1)=0,因此F′(1)=0且F′(x)有唯一的零点1.
当0<x<1时,F′(x)<0,当x>1时,F′(x)>0.
∴F(x)在(0,1)上为减函数,在(1,+∞)上为增函数,
∴F(x)的最小值为F(1)=0.
∴函数F(x)=x-$\frac{f(x)}{x}$有且只有一个零点.
点评 本题考查利用导数研究函数的单调性,训练了函数零点存在性定理的用法,考查逻辑思维能力与运算能力,是压轴题.

| A. | 向左平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向右平移$\frac{π}{2}$个单位 |
| A. | 命题“?x0∈R,x02-x0≤0”的否定为“?x∈R,x2-x>0” | |
| B. | 命题“在△ABC中,A>30°,则sinA>$\frac{1}{2}$”的逆否命题为真命题 | |
| C. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 | |
| D. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|+|{\overrightarrow b}$|,则$\overrightarrow a$与$\overrightarrow b$共线 |
| A. | $-\frac{11}{13}$ | B. | $-\frac{11}{12}$ | C. | $-\frac{7}{12}$ | D. | $-\frac{1}{13}$ |
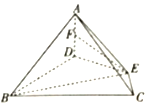 如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.