题目内容
4.已知实数x,y满足$\left\{\begin{array}{l}{3x+2y-12≤0}\\{x≥2}\\{y≥\frac{3}{2}}\end{array}\right.$,则$\frac{xy}{{x}^{2}{+y}^{2}}$的取值范围是( )| A. | [2,$\frac{5}{2}$] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | (0,$\frac{1}{2}$] | D. | [$\frac{2}{5}$,$\frac{1}{2}$] |
分析 画出约束条件的可行域,求出$\frac{y}{x}$的范围,化简目标函数,转化为函数的值域,求解即可.
解答 解:实数x,y满足$\left\{\begin{array}{l}{3x+2y-12≤0}\\{x≥2}\\{y≥\frac{3}{2}}\end{array}\right.$的可行域如图: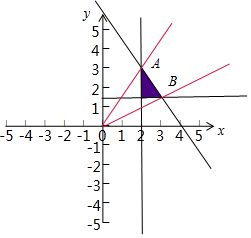
由图形可知:$\frac{y}{x}$的最小值:KOB,最大值是KOA,由$\left\{\begin{array}{l}{x=2}\\{3x+2y-12=0}\end{array}\right.$解得A(2,3),由$\left\{\begin{array}{l}{y=\frac{3}{2}}\\{3x+2y-12=0}\end{array}\right.$可得B(3,$\frac{3}{2}$),KOB=$\frac{1}{2}$,KOA=$\frac{3}{2}$,
则$\frac{xy}{{x}^{2}{+y}^{2}}$=$\frac{1}{\frac{x}{y}+\frac{y}{x}}$,令t=$\frac{y}{x}$,t∈$[\frac{1}{2},\frac{3}{2}]$,g(t)=$\frac{1}{t}$+t≥2,等号成立的条件是t=1,1∈[$\frac{1}{2}$,$\frac{3}{2}$],当t=$\frac{1}{2}$时,g($\frac{1}{2}$)=$\frac{5}{2}$,当t=$\frac{3}{2}$时,g($\frac{3}{2}$)=$\frac{13}{6}$,
可得$\frac{xy}{{x}^{2}{+y}^{2}}$=$\frac{1}{\frac{x}{y}+\frac{y}{x}}$∈[$\frac{2}{5}$,$\frac{1}{2}$].
故选:D.
点评 本题考查线性规划的简单应用,考查数形结合以及转化思想的应用,考查计算能力.

| 地区 | A | B | C |
| 数量 | 100 | 50 | 150 |
(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |