题目内容
2．${∫}_{0}^{3}$[$\sqrt{9-（x-3）^{2}}$-x]dx=$\frac{9π-8}{2}$．分析 根据定积分的计算和定积分的几何意义分别计算即可．
解答 解：${∫}_{0}^{3}$[$\sqrt{9-（x-3）^{2}}$dx表示以（3，0）为圆心，以3为半径的圆的面积二分之一，
故${∫}_{0}^{3}$[$\sqrt{9-（x-3）^{2}}$dx=$\frac{9π}{2}$，
${∫}_{0}^{3}$xdx=$\frac{1}{2}$x2|${\;}_{0}^{3}$=$\frac{8}{2}$，
则${∫}_{0}^{3}$[$\sqrt{9-（x-3）^{2}}$-x]dx=${∫}_{0}^{3}$[$\sqrt{9-（x-3）^{2}}$dx+${∫}_{0}^{3}$xdx=$\frac{9π-8}{2}$，
故答案为：$\frac{9π-8}{2}$
点评 本题考查了定积分的计算和定积分的几何意义，属于基础题．
练习册系列答案
相关题目
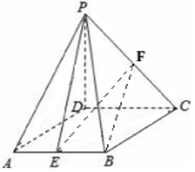如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠DAB=60°，PD⊥平面ABCD，PD=AD=1，点E、F分别为AB和PC的中点，连接EF、BF．