题目内容
2.要得到函数y=2sin(2x+$\frac{2π}{3}$)的图象,需要将函数y=2sin2x的图象( )| A. | 向左平移$\frac{2π}{3}$个单位 | B. | 向右平移$\frac{2π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
分析 由左加右减上加下减的原则可确定函数y=2sin2x到y=2sin(2x+$\frac{2π}{3}$)的路线,进行平移变换,推出结果.
解答 解:将函数y=2sin2x向左平移$\frac{π}{3}$个单位,即可得到y=2sin[2(x+$\frac{π}{3}$)]=2sin(2x+$\frac{2π}{3}$)的图象.
故选:C.
点评 本题主要考查三角函数的平移.三角函数的平移原则为左加右减上加下减,注意x的系数.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
10.欲证$\sqrt{7}$-1>$\sqrt{11}$-$\sqrt{5}$,只需证( )
| A. | ${(\sqrt{7}-1)^2}>{(\sqrt{11}-\sqrt{5})^2}$ | B. | ${(\sqrt{7}+1)^2}>{(\sqrt{11}+\sqrt{5})^2}$ | C. | ${(\sqrt{7}+\sqrt{5})^2}>{(\sqrt{11}+1)^2}$ | D. | ${(\sqrt{7}-\sqrt{5})^2}>{(\sqrt{11}-1)^2}$ |
12.如图是某几何体的三视图,则该几何体的体积是( )
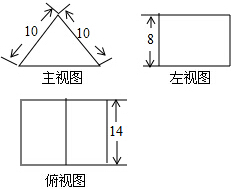

| A. | 672 | B. | 1120 | C. | 1344 | D. | 2016 |
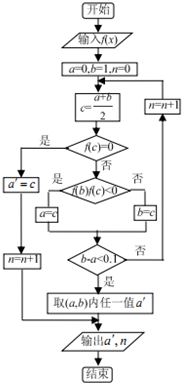 如图是用二分法求函数f(x)在区间(a,b)上的零点的程序框图,若输入的函数为f(x)=log2x+x-$\frac{1}{2}$,则输出的n的值为( )
如图是用二分法求函数f(x)在区间(a,b)上的零点的程序框图,若输入的函数为f(x)=log2x+x-$\frac{1}{2}$,则输出的n的值为( )