题目内容
19.已知sinα=$\frac{2}{3}$,cosβ=-$\frac{3}{4}$,且α、β∈($\frac{π}{2}$,π),判断α-β是第几象限角?分析 由条件求得α-β∈(-$\frac{π}{12}$,$\frac{π}{12}$ ),再根据sin(α-β)<0,求得α-β是第几象限角.
解答 解:∵sinα=$\frac{2}{3}$∈($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),cosβ=-$\frac{3}{4}$∈(-$\frac{\sqrt{3}}{2}$,-$\frac{\sqrt{2}}{2}$ ),且α、β∈($\frac{π}{2}$,π),
∴α∈($\frac{3π}{4}$,$\frac{5π}{6}$)、β∈($\frac{3π}{4}$,$\frac{5π}{6}$ ),
∴α-β∈(-$\frac{π}{12}$,$\frac{π}{12}$ ).
再根据cosα=-$\sqrt{{1-sin}^{2}α}$=-$\frac{\sqrt{5}}{3}$,sinβ=$\sqrt{{1-cos}^{2}β}$=$\frac{\sqrt{7}}{4}$,
可得sin(α-β)=sinαcosβ-cosαsinβ=$\frac{2}{3}•(-\frac{3}{4})$-(-$\frac{\sqrt{5}}{3}$)•$\frac{\sqrt{7}}{4}$=$\frac{-6+\sqrt{35}}{12}$<0,
可得α-β∈(-$\frac{π}{12}$,0),故α-β为第四象限角.
点评 本题主要考查三角函数在各个象限中的符号,两角差的正弦公式、同角三角函数的基本关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知集合M={(x,y)|x2+y2≤1},若实数λ,μ满足:对任意的(x,y)∈M,都有(λx,μy)∈M,则称(λ,μ)是集合M的“和谐实数对”.则以下集合中,存在“和谐实数对”的是( )
| A. | {(λ,μ)|λ+μ=4} | B. | {(λ,μ)|λ2+μ2=4} | C. | {(λ,μ)|λ2-4μ=4} | D. | {(λ,μ)|λ2-μ2=4} |
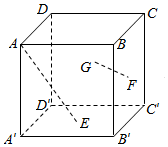 在正方体ABCD-A′B′C′D′中,E,F,G分别是面A′C′,面B′C,面CD′的中心,则AE与FG所成的角大小为多少?
在正方体ABCD-A′B′C′D′中,E,F,G分别是面A′C′,面B′C,面CD′的中心,则AE与FG所成的角大小为多少?