题目内容
如图,在底面是直角梯形的四棱锥S-ABCD中,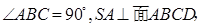


(1)求四棱锥S-ABCD的体积;
(2)求证: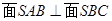
(3)求SC与底面ABCD所成角的正切值。
(1)2; (2)见解析;(3)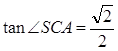
解析试题分析:(1)底面是直角梯形,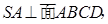 ,
,
可知SA是棱锥的高,根据公式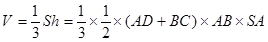 ,
,
把数据代入即可;
(2)根据题设,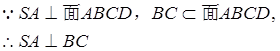
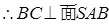 ,
, ;
;
(3)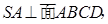 ,连接AC,显然
,连接AC,显然 就是SC与底面ABCD所成的角得平面角,
就是SC与底面ABCD所成的角得平面角,
在直角三角形SCA中,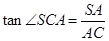 .
.
试题解析:(1)解: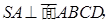 ,得SA是棱锥的高,
,得SA是棱锥的高,
又ABCD是直角梯形,
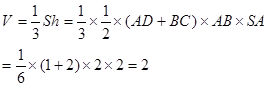
(2)证明:
又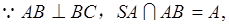
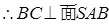
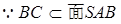

(3)解:已知,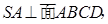 ,连结AC,则
,连结AC,则 就是SC与底面ABCD所成的角的平面角,则 在直角三角形SCA中,SA=2,,AC=
就是SC与底面ABCD所成的角的平面角,则 在直角三角形SCA中,SA=2,,AC= ,
,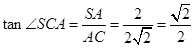
考点:棱锥体积,面面垂直,线面所成的角,是个综合题.

练习册系列答案
相关题目
 中,
中,
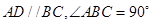 ,
,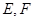 分别为边
分别为边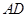 和
和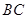 上的点,且
上的点,且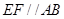 ,
,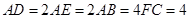 .将四边形
.将四边形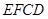 沿
沿 折起成如图2的位置,使
折起成如图2的位置,使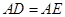 .
.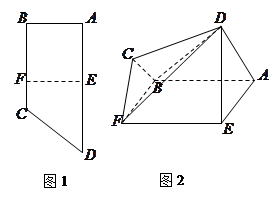
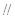 平面
平面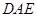 ;
; 的体积.
的体积.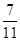
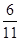
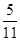
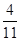
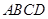 是菱形,
是菱形,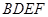 是矩形,
是矩形,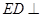 面
面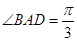 .
.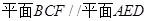 .
.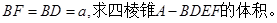

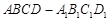 的棱长为
的棱长为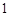 .
.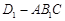 的左视图的面积;
的左视图的面积;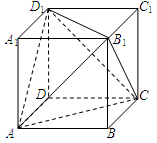
 中,底面
中,底面 为正方形,
为正方形,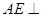 平面
平面 ,已知
,已知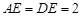 ,
,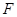 为线段
为线段 的中点.
的中点.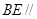 平面
平面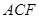 ;
;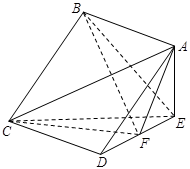
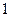 的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是
的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是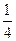 ,则此长方体的体积是 .
,则此长方体的体积是 . 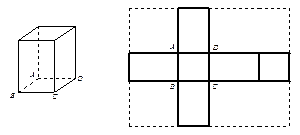
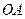 为球
为球 的半径,过
的半径,过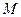 且垂直于
且垂直于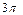 ,则球
,则球