题目内容
已知空间4个球,它们的半径分别为2, 2, 3, 3,每个球都与其他三个球外切,另有一个小球与这4个球都外切,则这个小球的半径为( )
A.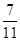 | B.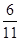 | C.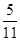 | D.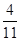 |
B
解析试题分析:设半径为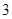 的两个球的球心为
的两个球的球心为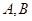 ,半径为2的两个球的球心为
,半径为2的两个球的球心为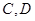 ,与这4个球都外切的小球的球心为
,与这4个球都外切的小球的球心为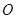 ,半径为
,半径为 ,连接
,连接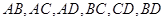 ,得到四棱锥
,得到四棱锥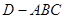 ,则
,则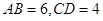 ,
,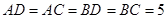 ,连接
,连接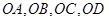 ,取
,取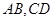 的中点分别为
的中点分别为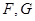 ,连接
,连接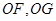 ,在
,在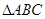 中,
中,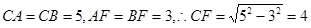 ,同理
,同理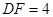 ,
,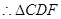 为等腰三角形,
为等腰三角形,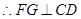 ,同理可证
,同理可证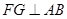 ,
,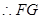 是异面直线
是异面直线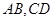 的公垂线,又
的公垂线,又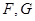 分别是
分别是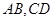 的中点,
的中点,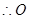 在线段
在线段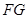 上,在
上,在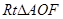 中,
中,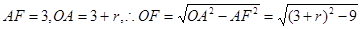 ,同理得
,同理得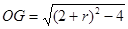 ,在
,在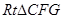 中,
中,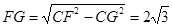 ,又
,又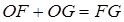 ,由此可得
,由此可得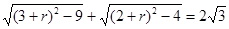 ,解得
,解得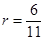 ,负值舍去。
,负值舍去。
考点:(1)空间两球相切的性质;(2)如何判断三点共线;(3)等腰三角形的性质;(4)异面直线公垂线的定义。

练习册系列答案
相关题目
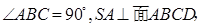


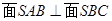
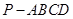 中,
中,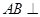 平面
平面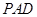 ,
,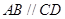 ,
,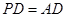 ,
,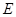 是
是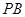 的中点,
的中点,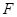 是
是 上的点且
上的点且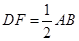 ,
,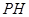 为△
为△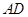 边上的高.
边上的高.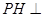 平面
平面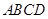 ;
;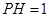 ,
,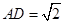 ,
,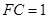 ,求三棱锥
,求三棱锥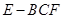 的体积;
的体积;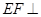 平面
平面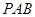 .
.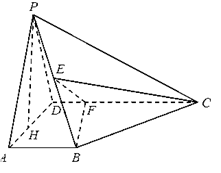
 中,
中, 平面
平面 .
.
 平面
平面 ;
; ,
, 为
为 中点,求三棱锥
中点,求三棱锥 的体积.
的体积.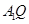 和
和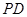 所成的角为
所成的角为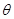 ,求
,求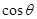 的值.
的值.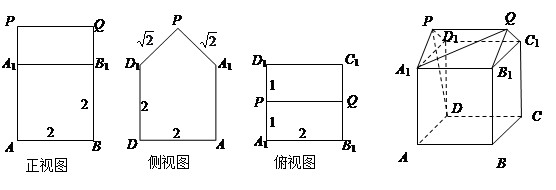

 ;
; 与
与 成
成 角;
角; 与
与 是异面直线;
是异面直线;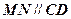 .
. ,底面周长为3,那么这个球的体积为 .
,底面周长为3,那么这个球的体积为 . 的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.