题目内容
10.在底面是正方形的长方体ABCD-A1B1C1D1中,MN是在平面ACCA${\;}_1^{\;}$内,且MN⊥AC,则MN和BB1的位置关系是平行.分析 利用底面是正方形的长方体ABCD-A1B1C1D1,证明MN⊥BD,根据MN⊥AC,证明MN⊥平面ABCD,利用BB1⊥平面ABCD,即可得出MN∥BB1.
解答 解:由长方体的性质知,AA1⊥平面ABCD,∴AA1⊥BD,
∵BD⊥AC,AA1∩AC=A,
∴BD⊥平面ACCA${\;}_1^{\;}$,
∵MN在平面ACCA${\;}_1^{\;}$内,
∴MN⊥BD,
∵MN⊥AC,∴MN⊥平面ABCD,
∵BB1⊥平面ABCD,
∴MN∥BB1,
故答案为:平行.
点评 本题考查线面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-1(x≥0)}\\{-2x(x<0)}\end{array}\right.$,则f(-1)=( )
| A. | 2 | B. | 0 | C. | -2 | D. | 1 |
19.已知a,b为实数,则( )
| A. | (a+b)2≤4ab,$a+b≤\sqrt{2{a^2}+2{b^2}}$ | B. | (a+b)2≥4ab,$a+b≤\sqrt{2{a^2}+2{b^2}}$ | ||
| C. | (a+b)2≤4ab,$a+b≥\sqrt{2{a^2}+2{b^2}}$ | D. | (a+b)2≥4ab,$a+b≥\sqrt{2{a^2}+2{b^2}}$ |
20.若某几何体的三视图如图所示,则此几何体的表面积为( )
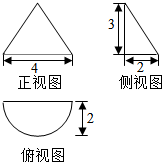

| A. | $(4+2\sqrt{13})π$ | B. | $6+(2+\sqrt{13})π$ | C. | $(\sqrt{13}+2)π$ | D. | $8+2\sqrt{13}π$ |
 如图,D是△ABC外接圆上的一点,弦AD与BC交于点E,且AB=AC=6,AE=4.
如图,D是△ABC外接圆上的一点,弦AD与BC交于点E,且AB=AC=6,AE=4.