题目内容
求函数y=
的定义域时,第一步推理中大前提是
有意义时,a≥0,小前提是
有意义,结论是 .
| log2x-2 |
| a |
| log2x-2 |
考点:演绎推理的基本方法
专题:推理和证明
分析:根据演绎推理的逻辑思路,当大前提是
有意义时,a≥0,小前提是
有意义,结论应为log2x-2≥0.
| a |
| log2x-2 |
解答:
解:根据演绎推理求函数y=
的定义域时,
若大前提是
有意义时,a≥0,
小前提是
有意义,
可知:结论应为:log2x-2≥0,
故答案为:log2x-2≥0.
| log2x-2 |
若大前提是
| a |
小前提是
| log2x-2 |
可知:结论应为:log2x-2≥0,
故答案为:log2x-2≥0.
点评:本题考查演绎推理--三段论,解题的关键是理解三段论的形式,本题是基础概念考查题.

练习册系列答案
相关题目
若a>b>0,c<d<0,则一定有( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
当a>l时,函数f (x)=logax和g(x)=(l-a)x的图象的交点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
当a=3时,下面的程序段输出的y是( )


| A、9 | B、3 | C、10 | D、6 |
一个四棱锥的三视图如图所示,则该四棱锥的侧面中,直角三角形的个数为( )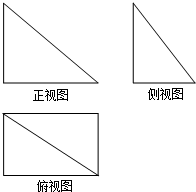

| A、1 | B、2 | C、3 | D、4 |
已知函数f(x)=x+
,则函数y=f(x)的大致图象为( )
| 1 |
| |x| |
A、 |
B、 |
C、 |
D、 |