题目内容
已知一个圆柱形的容器内放置了一个与底面与侧面都相切的玻璃球，在这个玻璃球的上面放置了三个半径为2的小玻璃珠，它们两两相切，且与大玻璃球及容器的侧面都相切，在小玻璃球面上任意取一点M，则点M到圆柱底面的距离的最大值是 ．
考点：球的体积和表面积
专题：综合题,空间位置关系与距离
分析：先作出图形，如图所示，则三棱锥的底面边长为4，求出圆柱和大球的半径，可得O到底面的距离，即可求出点M到圆柱底面的距离的最大值
解答：
解：先作出图形，如图所示，则三棱锥的底面边长为4，
设圆柱和大球的半径为R，则侧棱长为2+R，
∴R=2+
×
×4=2+
，
∴O到底面的距离为
=
，
∴点M到圆柱底面的距离的最大值是4+
+
．
故答案为：4+
+
．
解：先作出图形，如图所示，则三棱锥的底面边长为4，设圆柱和大球的半径为R，则侧棱长为2+R，
∴R=2+
| 2 |
| 3 |
| ||
| 2 |
4
| ||
| 3 |
∴O到底面的距离为
(R+2)2-(
|
| 4 |
| 3 |
9+6
|
∴点M到圆柱底面的距离的最大值是4+
4
| ||
| 3 |
| 4 |
| 3 |
9+6
|
故答案为：4+
4
| ||
| 3 |
| 4 |
| 3 |
9+6
|
点评：本题考查点M到圆柱底面的距离的最大值，考查学生的计算能力，属于中档题．
练习册系列答案
特高级教师点拨系列答案
相关题目
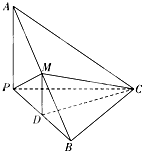如图，已知三棱锥A-BPC中，AP⊥PC，PC⊥BC，M为AB的中点，D为PB的中点，且△PMB为正三角形．