题目内容
 如图所示,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,E是PB的中点,PD=AD.
如图所示,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,E是PB的中点,PD=AD.(1)求证:平面PAC⊥平面PBD;
(2)求证:PC⊥平面ADE;
(3)求二面角A-ED-B的大小.
考点:二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)由线面垂直得AC⊥PD,由正方形性质得AC⊥BD,由此能证明平面PAC⊥平面PBD.
(2)根据线面垂直的判定定理即可证明PC⊥平面ADE.
(3)作辅助线,寻找二面角的平面角,然后根据三角形的边角关系即可求出二面角的大小.
(2)根据线面垂直的判定定理即可证明PC⊥平面ADE.
(3)作辅助线,寻找二面角的平面角,然后根据三角形的边角关系即可求出二面角的大小.
解答:
(1)证明:∵PD⊥底面ABCD,AC?底面ABCD,
∴AC⊥PD,
又∵底面ABCD为正方形,
∴AC⊥BD,而PD与BD交于点D,
∴AC⊥平面PBD,
又AC?平面PAC,
∴平面PAC⊥平面PBD.
(2)解:取PC的中点F,
∵PD=DC,∴PC⊥DF,
∵PD⊥底面ABCD,
∴DC是PC在底面ABCD上的射影,
则PC⊥AD,
∵AD∩DF=D,
∴PC⊥面ADF,
∵E是PB的中点,∴EF∥BC∥AD,即A,E,F,D共面,
∴PC⊥面ADE.
(3)解:设AC∩BD=O,作OM⊥DE于M,连结AM,
∵AO⊥面PBD,
∴由三垂线定理,AM⊥DE,
即∠AMO是二面角A-ED-B的平面角,
在Rt△OMD中,OM=ODsin∠MDO=DOsin∠PBD=
AD×
=
AD=
AO,
在Rt△AOM中,tan∠AMO=
=
,
即∠AMO=60°.
∴AC⊥PD,
又∵底面ABCD为正方形,
∴AC⊥BD,而PD与BD交于点D,
∴AC⊥平面PBD,
又AC?平面PAC,
∴平面PAC⊥平面PBD.
(2)解:取PC的中点F,
∵PD=DC,∴PC⊥DF,
∵PD⊥底面ABCD,
∴DC是PC在底面ABCD上的射影,
则PC⊥AD,
∵AD∩DF=D,

∴PC⊥面ADF,
∵E是PB的中点,∴EF∥BC∥AD,即A,E,F,D共面,
∴PC⊥面ADE.
(3)解:设AC∩BD=O,作OM⊥DE于M,连结AM,
∵AO⊥面PBD,
∴由三垂线定理,AM⊥DE,
即∠AMO是二面角A-ED-B的平面角,
在Rt△OMD中,OM=ODsin∠MDO=DOsin∠PBD=
| ||
| 2 |
| ||
| 3 |
| ||
| 6 |
| ||
| 3 |
在Rt△AOM中,tan∠AMO=
| AO |
| OM |
| 3 |
即∠AMO=60°.
点评:本题主要考查空间直线和平面垂直,面面垂直的判定,以及二面角的求解,要求熟练掌握相应的判定定理,以及二面角的求解方法.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,f(x)=
则函数g(x)=4f(x)-1的零点个数为( )
|
| A、4 | B、6 | C、8 | D、10 |
某厂1998年的产值为a万元,预计产值每年以n%递增,则该厂到2010年的产值(单位:万元)是( )
| A、a(1+n%)13 | ||
| B、a(1+n%)12 | ||
| C、a(1+n%)11 | ||
D、
|
 函数f(x)=Asin(ωx+φ)(其中ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中ω>0,|φ|<| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
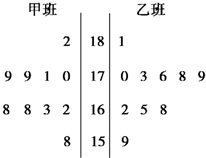 随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.