题目内容
已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,f(x)=
则函数g(x)=4f(x)-1的零点个数为( )
|
| A、4 | B、6 | C、8 | D、10 |
考点:分段函数的应用
专题:函数的性质及应用
分析:由g(x)=4f(x)-1=0,得f(x)=
,作出函数f(x)的表达式,利用数形结合即可得到结论.
| 1 |
| 4 |
解答:
 解:由g(x)=4f(x)-1=0,得f(x)=
解:由g(x)=4f(x)-1=0,得f(x)=
,
要判断函数g(x)的零点个数,则根据f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,
只需要判断当x>0时f(x)=
的个数即可,
当0<x≤2时,f(x)=2|x-1|-1∈[0,1],
当2<x≤4时,0<x-2≤2时,f(x)=
f(x-2)=
[2|x-3|-1]∈[0,
],
当4<x≤6时,2<x-2≤4时,f(x)=
f(x-2)=
[2|x-5|-1]∈[0,
],
当6<x≤8时,4<x-2≤6时,f(x)=
f(x-2)=
[2|x-7|-1]∈[0,
],
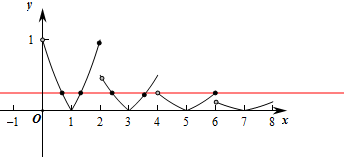
作出函数f(x)在(0,8)上的图象,由图象可知f(x)=
有5个根,
则根据偶函数的对称性可知f(x)=
在定义域(-∞,0)∪(0,+∞)上共有10个根,
即函数g(x)=4f(x)-1的零点个数为10个,
故选:D
 解:由g(x)=4f(x)-1=0,得f(x)=
解:由g(x)=4f(x)-1=0,得f(x)=| 1 |
| 4 |
要判断函数g(x)的零点个数,则根据f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,
只需要判断当x>0时f(x)=
| 1 |
| 4 |
当0<x≤2时,f(x)=2|x-1|-1∈[0,1],
当2<x≤4时,0<x-2≤2时,f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当4<x≤6时,2<x-2≤4时,f(x)=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
当6<x≤8时,4<x-2≤6时,f(x)=
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
作出函数f(x)在(0,8)上的图象,由图象可知f(x)=
| 1 |
| 4 |
则根据偶函数的对称性可知f(x)=
| 1 |
| 4 |
即函数g(x)=4f(x)-1的零点个数为10个,
故选:D
点评:本题主要考查函数零点的个数判断,利用函数和方程之间的关系转化为两个函数的交点个数问题,利用分段函数的表达式,作出函数f(x)的图象是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
下列值等于1的积分是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=(
)x-log3x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值( )
| 1 |
| 5 |
| A、不小于0 | B、恒为正数 |
| C、恒为负数 | D、不大于0 |
集合M={x|x=
+
,k∈A},集合N={x|x=
+
,k∈z},则( )?
| k |
| 2 |
| 1 |
| 4 |
| k |
| 4 |
| 1 |
| 2 |
| A、M=N | B、M≠N |
| C、M≠N | D、M?N |
已知函数f(x)=x3-3x2-sinπx,则f(
)+f(
)+…+f(
)+f(
)=( )
| 1 |
| 2013 |
| 2 |
| 2013 |
| 4024 |
| 2013 |
| 4025 |
| 2013 |
| A、4025 | B、-4025 |
| C、8050 | D、-8050 |
函数f(x)=
的图象大致为( )
| 1 |
| ln(x+1)-x |
A、 |
B、 |
C、 |
D、 |
使圆x2+y2=r2与x2+y2+2x-4y+4=0有交点的充要条件是( )
A、r<
| ||
B、r>
| ||
C、|r-
| ||
D、|r-
|
 如图所示,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,E是PB的中点,PD=AD.
如图所示,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,E是PB的中点,PD=AD.