题目内容
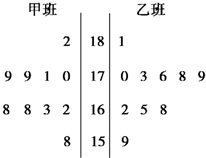 随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.(1)计算甲班的样本方差;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
考点:茎叶图,极差、方差与标准差,古典概型及其概率计算公式
专题:概率与统计
分析:(1)由茎叶图先求出甲班样本平均数,再求甲班的样本方差.
(2)设“身高为176cm的同学被抽中”为事件A.从乙班10名同学中抽取两名身高不低于173cm的同学有10个基本事件,而事件A含有4个基本事件,由此能求出身高为176cm的同学被抽中的概率.
(2)设“身高为176cm的同学被抽中”为事件A.从乙班10名同学中抽取两名身高不低于173cm的同学有10个基本事件,而事件A含有4个基本事件,由此能求出身高为176cm的同学被抽中的概率.
解答:
解:(1)
=
=170.
甲班的样本方差s2=
[(158-170)2+(162-170)2+(163-170)2
+(168-170)2+(168-170)2+(170-170)2+(171-170)2
+(179-170)2+(179-170)2+(182-170)2]=57.2.
(2)设“身高为176 cm的同学被抽中”为事件A.
从乙班10名同学中抽取两名身高不低于173 cm的同学有:
(181,173),(181,176),(181,178),
(181,179),(179,173),(179,176),
(179,178),(178,173),(178,176),(176,173),
共10个基本事件,
而事件A含有4个基本事件:
(181,176),(179,176),(178,176),(176,173).
所以P(A)=
=
.
. |
| x |
| 158+162+163+168+168+170+171+179+179+182 |
| 10 |
甲班的样本方差s2=
| 1 |
| 10 |
+(168-170)2+(168-170)2+(170-170)2+(171-170)2
+(179-170)2+(179-170)2+(182-170)2]=57.2.
(2)设“身高为176 cm的同学被抽中”为事件A.
从乙班10名同学中抽取两名身高不低于173 cm的同学有:
(181,173),(181,176),(181,178),
(181,179),(179,173),(179,176),
(179,178),(178,173),(178,176),(176,173),
共10个基本事件,
而事件A含有4个基本事件:
(181,176),(179,176),(178,176),(176,173).
所以P(A)=
| 4 |
| 10 |
| 2 |
| 5 |
点评:本题考查样本方差的求法,考查概率的求法,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
已知函数f(x)=x3-3x2-sinπx,则f(
)+f(
)+…+f(
)+f(
)=( )
| 1 |
| 2013 |
| 2 |
| 2013 |
| 4024 |
| 2013 |
| 4025 |
| 2013 |
| A、4025 | B、-4025 |
| C、8050 | D、-8050 |
程序框图如图所示,其输出结果是63,则a的初始值m,(m>0)有多少种可能( )


| A、3 | B、4 | C、5 | D、6 |
四面体S-ABC中,各个侧面都是边长为a的正三角形,则异面直线SA与BC所成的角等于( )
| A、90° | B、60° |
| C、45° | D、30° |
 如图所示,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,E是PB的中点,PD=AD.
如图所示,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,E是PB的中点,PD=AD.