题目内容
已知α,β∈(0,π),且tan(α-β)=
,tanβ=-
(1)计算tanα、tan2α的值
(2)求2α-β的值.
| 1 |
| 2 |
| 1 |
| 7 |
(1)计算tanα、tan2α的值
(2)求2α-β的值.
考点:两角和与差的正切函数
专题:计算题,三角函数的求值
分析:(1)利用差角的正切公式,求出tanα;利用二倍角公式求出tan2α的值;
(2)先求出tan(2α-β)=1,再确定-π<2α-β<0,即可求2α-β的值.
(2)先求出tan(2α-β)=1,再确定-π<2α-β<0,即可求2α-β的值.
解答:
解:(1)∵tan(α-β)=
,∴
=
…(2分)
而:tanβ=-
,∴
=
,解得tanα=
…(5分)
∴tan2α=
=
=
…(7分)
(2)tan(2α-β)=
=
=1.…(9分)
∵tanα=
>0,α∈(0,π),∴0<α<
,0<2α<π
∵tan2α=
>0∴0<2α<
,…(11分)
∵tanβ=-
<0,β∈(0,π),∴
<β<π,…(12分)
∴-π<2α-β<0,…(13分)
∴2α-β=-
. …(15分)
| 1 |
| 2 |
| tanα-tanβ |
| 1+tanαtanβ |
| 1 |
| 2 |
而:tanβ=-
| 1 |
| 7 |
tanα+
| ||
1-
|
| 1 |
| 2 |
| 1 |
| 3 |
∴tan2α=
| 2tanα |
| 1-tan2α |
2×
| ||
1-(
|
| 3 |
| 4 |
(2)tan(2α-β)=
| tan2α-tanβ |
| 1+tan2αtanβ |
| ||||
1-
|
∵tanα=
| 1 |
| 3 |
| π |
| 2 |
∵tan2α=
| 3 |
| 4 |
| π |
| 2 |
∵tanβ=-
| 1 |
| 7 |
| π |
| 2 |
∴-π<2α-β<0,…(13分)
∴2α-β=-
| 3π |
| 4 |
点评:本题考查两角和与差的正切函数,考查知值求角,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
经过圆C:(x+1)2+(y-2)2=4的圆心且倾斜角为
的直线方程为( )
| 3π |
| 4 |
| A、x-y+3=0 |
| B、x-y-3=0 |
| C、x+y-1=0 |
| D、x+y+3=0 |
已知条件p:
≤1,条件q:x≤1,则q是¬p成立的( )条件.
| 1 |
| x |
| A、充分不必要 | B、必要不充分 |
| C、充要 | D、非充分非必要 |
已知函数f(x)(x∈R)满足f(2)=3,且f′(x)<1,则不等式f(x2)<x2+1的解集是( )
A、(-∞,-
| ||||
B、(
| ||||
C、(-
| ||||
D、(-∞,-
|
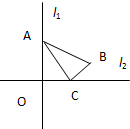 已知△ABC中,A,B,C的对边分别为a,b,c,且
已知△ABC中,A,B,C的对边分别为a,b,c,且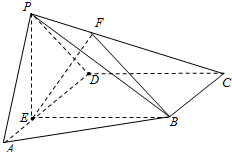 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.